第二类换元法中,最常用的是三角代换。
1,第一类换元:\(u=g(x)\qquad\int f(g(x))g'(x)dx=\int f(u)du\),我们是将一个 \(x\) 的函数 \(g(x)\) 换成一个变量 \(u\);
2,第二类换元:\(x=\phi(t)\qquad\int f(x)dx=\int f(\phi(t))\phi(t)dt\),我们是将自变量 \(x\) 换成另一个变量的函数 \(x=\phi(t)\)。
第二类换元法里,最常用的是三角代换。我们对于形如 \(\sqrt{a^2-x^2},\sqrt{x^2+a^2},\sqrt{x^2-a^2}\) 的积分,利用三角代换,可以利用三角函数的平方和公式,将根式去掉,从而简化积分。
3,三角代换:
(1)\(\sqrt{a^2-x^2}\),令\(x=a\sin t\),\(\sqrt{a^2-x^2}=\sqrt{a^2-a^2\sin^2 t}=a\cos t\),\(dx=a\cos tdt\)
(2)\(\sqrt{a^2+x^2}\),令\(x=a\tan t\),\(\left(1+\tan^2 t=\sec^2 t\right)\sqrt{a^2+x^2}=a\sec t, dx=a\sec^2tdt\)
(3)\(\sqrt{x^2-a^2}\),令\(x=a\sec t\),\(\left(1+\tan^2 t=\sec^2 t\right)\sqrt{x^2-a^2}=a\tan t, dx=a\tan t\sec tdt\)
例1,求\(\displaystyle\int \frac{\sqrt{9-x^2}}{x^2}dx\)
解:令\(x=3\sin t\),则\(dx=3\cos tdt\)
\[\begin{align*}\int \frac{\sqrt{9-x^2}}{x^2}dx&=\int \frac{\sqrt{9-9\sin^2 t}}{9\sin^2 t}\cdot\cos tdt\\ &=\int \frac{3\cos t\cdot 3\cos t}{9 \sin^2 t}dt=\int \frac{\cos^2 t}{\sin^2 t}dt\\ &=\int \cot^2 tdt\end{align*}\]
又因\(\cot^2 t+1=\csc^2t\),
\[\int \cot^2 tdt=\int (csc^2 t-1)dt=-\cot t-t+C\]
要换回\(x\),利用直角三角形,\(x=3\sin t, \sin t=\frac{x}{3}, t=\arcsin\frac{x}{3}, \cot t=\frac{\sqrt{9-x^2}}{x}\)
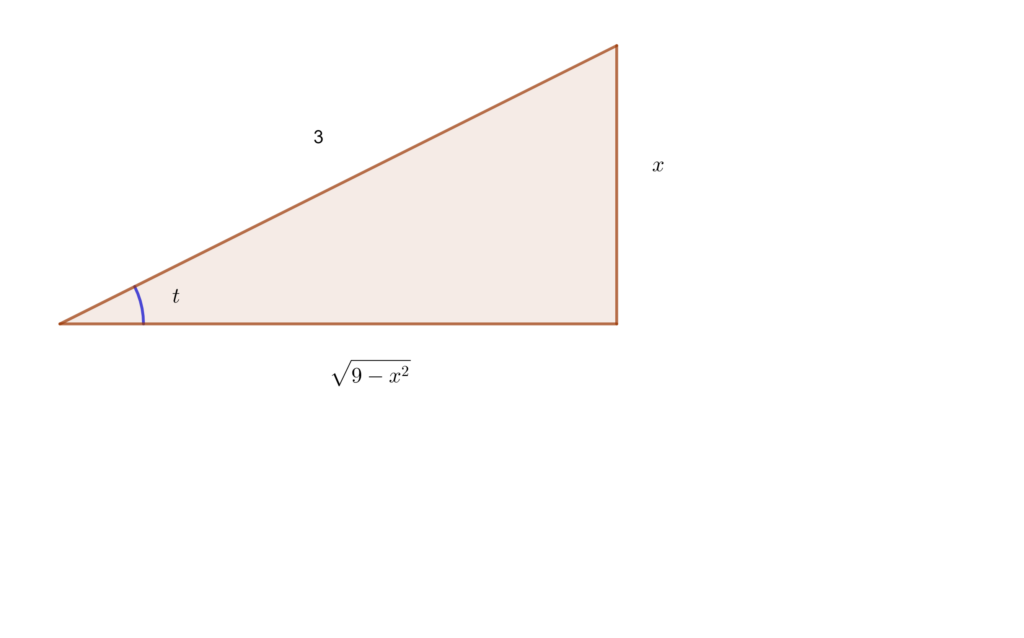
所以,
\[\int \frac{\sqrt{9-x^2}}{x^2}dx=-\frac{9-x^2}{x}-\arcsin\frac{x}{3}+C\]
例2,求\(\displaystyle\int \frac{dx}{x^2\sqrt{x^2+4}}\)
解:令\(x=2\tan t\),则\(dx=2\sec^2 tdt\),
\[\begin{align*}\int \frac{dx}{x^2\sqrt{x^2+4}}&=\int \frac{2\sec^2 tdt}{4\tan^2t\sqrt{4\tan^2\cdot t\cdot\sec t}}=\int \frac{\sec t}{4\tan^2 t}dt\\ &=\frac{1}{4}\int \frac{1}{\cos t}\cdot\frac{cos^2 t}{\sin^2 t}dt=\frac{1}{4}\int \frac{\cos t}{\sin^2 t}dt\\ &=\frac{2}{4}\int \cot t\cdot\csc tdt=\frac{1}{4}\csc t+C\end{align*}\]
回代,利用直角三角形,
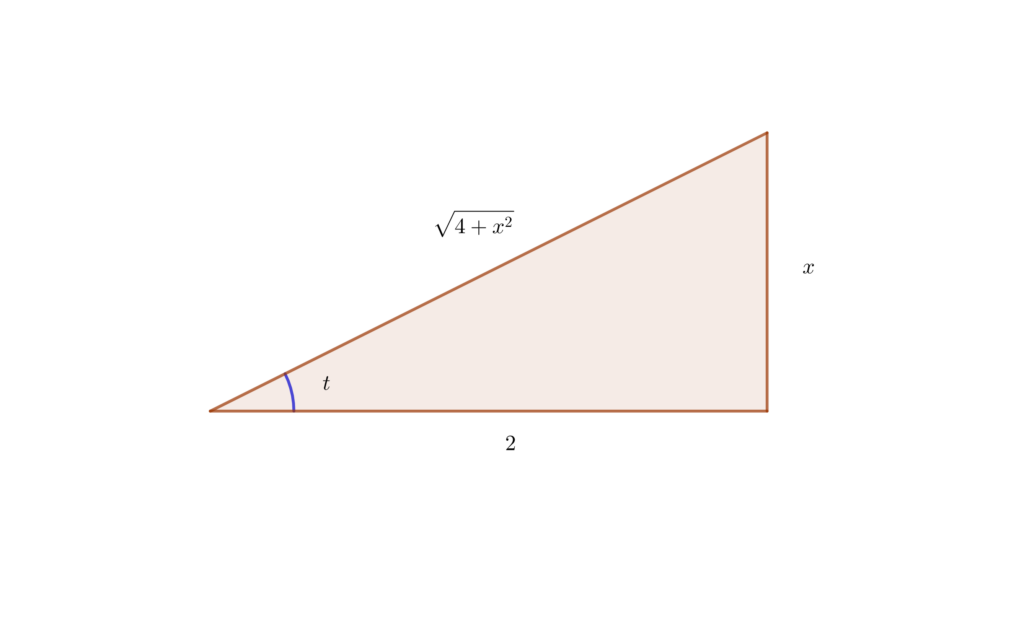
可以得到,\( x=2\tan t, \tan t=\frac{x}{2},\csc t=\frac{\sqrt{4+x^2}}{x}\),所以
\[\int \frac{dx}{x^2\sqrt{x^2+4}}=-\frac{1}{4}\cdot\frac{\sqrt{4+x^2}}{x}+C\]
例3,求\(\displaystyle\int \frac{dx}{\sqrt{x^2-a^2}}\)
解:令\(x=a\sec t\),则\(dx=a \sec t\tan t dt\),
\[\begin{align*}\int \frac{dx}{\sqrt{x^2-a^2}}&=\int \frac{a \sec t\tan t dt}{\sqrt {a^2 \sec^2 t-a^2}}=\frac{1}{a}\int \frac{a \sec t\tan t}{\tan t}dt\\ & =\int \sec tdt=\int \frac{1}{\sin t}dt =\int \frac{\sin t}{\sin^2 t}dt\\ &=\int \frac{\sin tdt}{1-\cos^2 t}\end{align*}\]
令\(u=\cos t\),则\(du=\sin tdt\)
则
\[\begin{align*}\displaystyle\int \frac{\sin tdt}{1-\cos^2 t}&=-\int \frac{du}{1-u^2}=-\frac{1}{2}\int \left(\frac{1}{1-u}-\frac{1}{1+u}\right)du\\ & =-\frac{1}{2}\left(-\ln|1-n|-\ln|1+n|\right)+C=\frac{1}{2}\ln |1-n^2|+C\\& =\frac{1}{2}\ln|\sin^2 t|+C=\ln |\sin t|+C\end{align*}\]
这里我们应用是部分分式分解\(\displaystyle\frac{1}{1-u^2}=1-\frac{1}{(1-u)(1+u)}=\frac{A}{1-u}+\frac{B}{1+u}\),得\(A(1+u)+B(1-u)=1\),我们将 \(u\) 分别用 \(1\) 和 \(-1\) 代入这个等式,得到
\[ u=1\qquad\Rightarrow\quad 2A=1,\quad A=\frac{1}{2}\]
\[ u=-1\qquad\Rightarrow\quad -2B=1,\quad B=-\frac{1}{2}\]
利用三角形代回原来变量:
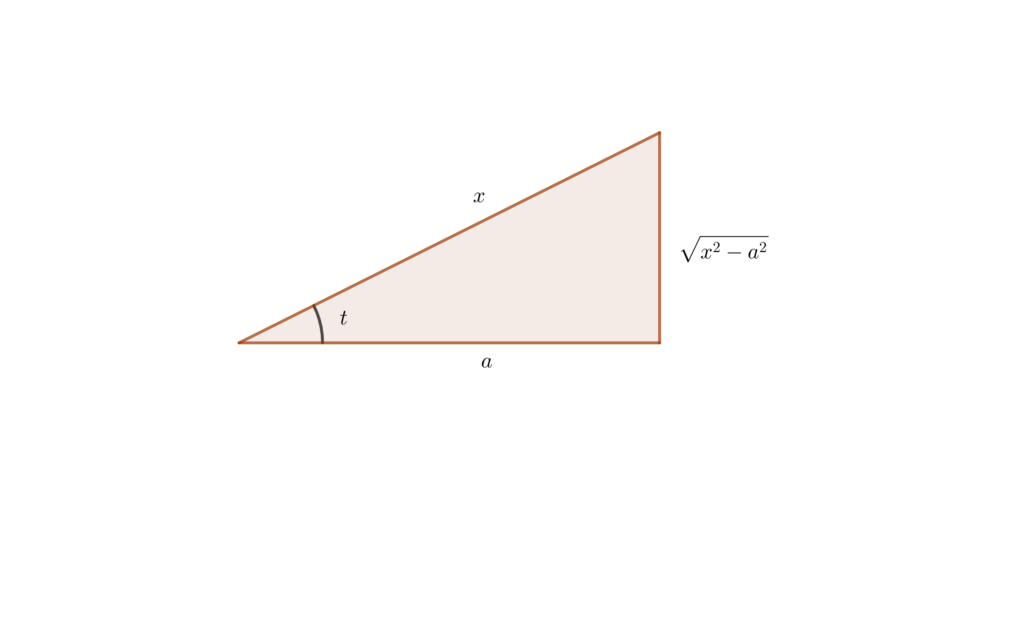
\(x=a\sec t\),则 \(\displaystyle\sec t=\frac{x}{a},\cos t=\frac{a}{x}, \sin t=\frac{\sqrt{x^2-a^2}}{x}\),所以
\[\int \frac{dx}{\sqrt{x^2-a^2}}=\ln|\frac{x^2-a^2}{x}|+C\]
例4,求\(\displaystyle\int \frac{dx}{\sqrt{1+x-x^2}}\)
解:先把\(\sqrt{-x^2+x+1}\)配方,
\[\begin{align*}\int \frac{dx}{\sqrt{1+x-a^2}}&=\int \frac{dx}{\sqrt{-(x^2-x)+1}}=\int \frac{dx}{\sqrt{-(x-\frac{1}{2})^2+\frac{1}{4}+1}}\\ &=\int \frac{dx}{\sqrt {\frac{5}{4}-(x-\frac{1}{2})^2}}=\int \frac{dx}{\sqrt {\left(\frac{\sqrt 5}{2}\right)^2-(x-\frac{1}{2})^2}}\end{align*}\]
令\(\displaystyle x-\frac{1}{2}=\frac {\sqrt 5}{2}\sin t\)
所以,\[\begin{align*}\int \frac{dx}{\sqrt {\left(\frac{\sqrt 5}{2}\right)^2-(x-\frac{1}{2})^2}}&=\int \frac{\frac{\sqrt 5}{2}\cos tdt}{\sqrt {\left(\frac{\sqrt 5}{2}\right)^2-\left(\frac{\sqrt 5}{2}\right)^2\sin^2 t}}\\&=\int \frac{\frac{\sqrt 5}{2}\cos tdt}{\frac{\sqrt 5}{2}\cos t}=\int dt=t+C\end{align*}\]
代回原来变量:\(\displaystyle\sin t=\frac{2(x-\frac{1}{2})}{\sqrt 5}\),则\(\displaystyle t=\arcsin \left(\frac{2x-1}{\sqrt 5}\right)\)
所以,
\[\displaystyle\int \frac{dx}{\sqrt{1+x-x^2}}=\arcsin \frac{2x-1}{\sqrt 5}+C\]
