1,变力做功:考虑变力 \(f(x)\) 沿着直线从 \(a\) 点移到 \(b\) 点所做的功,

我们对将区间 \([a,b]\) 划分成 \(n\) 个子区间,在每一个子区间上,变力可以用常力近似,我们取区间上任意一点的值 \(f(x_i^*)\) 做为区间上力的代表,那么第 \(i\) 个子区间的功为
\[\Delta w_i\approx f(x_i^*)\Delta x_i\]
整个区间上变力所做的功为
\[w=\sum_{i=1}^n\Delta w_i\approx \sum_{i=1}^n\Delta w_if(x_i^*)\Delta x_i\]
当每一个子区间的长度趋近于 \(0\) 时,上式的极限就是变力所做的功。即
\[w=\lim_{\Delta x\to 0}\sum_{i=1}^n\Delta w_if(x_i^*)\Delta x_i\]
这是和式的极限,就是定积分,所以
\[w=\int_a^bf(x)dx\]
例1:将一个粒子从 \(x=1\) 移动到 \(x=3\),使用的力为 \(f(x)=x^2+2x\),求此力所做的功。
解:由上面的推导,
\[\begin{align*}w&=\int_1^3(x^2+2x)dx=\frac{x^3}{3}+x^2\Big|_1^3=\frac{50}{3}\end{align*}\]
例2:圆锥形的水罐,顶部半径为 \(8m\),高 \(10m\),当水位为 \(8m\) 时,将水抽空需要做多少功?
解:我们记 \(x\) 为从顶部朝下的距离,我们将区间划分成 \(n\) 个小区间,在每一个小区间上,所做的功就是将一薄层水提升距离 \(x\) 所做的功,
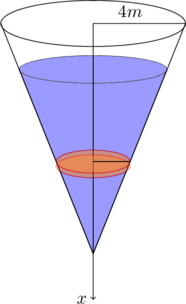
我们要先求出这一层水的体积,因为区间长度很小,这一层水可以看成是圆柱体。取这区间上任意一点 \(x_i^*\),以这点处的半径作为圆柱体的半径,由相似三角形的关系,
\[\frac{r_i^*}{4}=\frac{10-x_i^*}{10},\quad r_i^*=\frac{2}{5}(10-x_i^8)\]
所以这一层水的体积近似为
\[\Delta V_i\approx\pi r_i^*^2\Delta x_i =\frac{4\pi}{25}(10-x_i^*)^2\Delta x_i\]
将这一层水提升所需要的力为
\[f(x_i^*)=9.8\cdot1000\cdot\frac{4\pi}{25}(10-x_i^*)^2\Delta x_i\]
因而,所所有的水抽空所做的功为
\[\begin{align*}w&=\int_2^{10} 9800\cdot\frac{4\pi}{25}(10-x)^2dx\\ &=-392\pi\frac{1}{3}(10-x)^3\Big|_2^{10}\\&=\frac{392\cdot8^3}{3}\end{align*}\]
所需要的功为 \(\frac{392\cdot8^3}{3}\) 焦耳。
