圆桶法是另一种求旋转体体积的方法,如果平面区域由 \(y=f(x),x=a,x=b\) 以及 \(x\) 轴围成,求它绕 \(y\) 轴旋转所得的旋转体的体积。这种情况,如果采用切片法,就要将 \(y=f(x)\) 表示成 \(x=h(y)\) 的形式,然后以 \(y\) 为积分变量求积分。但是,若 \(f(x)\) 的反函数不存在,或者它的反函数很复杂,那切片法求体积就不合适了。这就需要使用圆桶法来求。
1,圆桶法求旋转体的体积。如果平面区域由 \(y=f(x),x=a,x=b\) 以及 \(x\) 轴围成,

求它绕 \(y\) 轴旋转所得的旋转体的体积。我们把区间划分成很多个子区间,考虑每一个子区间上旋转体的体积
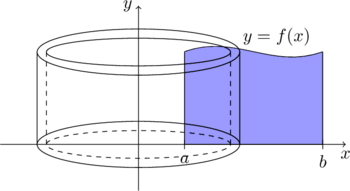
这个小区间上旋转体的体积可以用圆桶壁的体积近似,我们用圆桶的外侧体积减去圆桶内侧的体积,就得到了圆桶壁的体积,所以
\[\Delta V_i\approx f(x_i^*)(\pi(x_{i-1}+\Delta x_i)^2-\pi(x_{i-1})^2)=2\pi x_{i-1}f(x_i^*)\Delta x_i+\pi f(x_i^*)\Delta^2x_i\]
略去高阶无穷小,\[\Delta V_i\approx 2\pi x_{i-1}f(x_i^*)\Delta x_i\]
所有这些子区间上的旋转体的体积加起来就是整个区间上旋转体的体积。然后将区间划分更细,使得每一个子区间的长度趋近于 \(0\),上述近似值的极限就是旋转体的体积的精确值,也就是和式的极限,就是定积分
\[V=\int_a^b2\pi xf(x)dx\]
同理,由 \(x=h(y), y=c,y=d\) 以及 \(y\) 轴所围成的区域绕 \(x\) 轴旋转所得的旋转体的体积为 \[\int_c^d2\pi yh(y)dy\]
我们来看例题。
例1:求由曲线 \(y=2x^2-x^3\) 和 \(y=0\) 所围成的图形绕 \(y\) 轴旋转所得的体积。
解:函数与 \(x\) 轴的交点为 \(2x^2-x^3=x^2(2-x)=0, x=0,2\)。区域的图形为
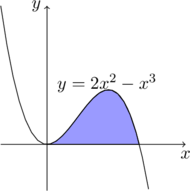
旋转体的体积为
\[\begin{align*}V&=\int_0^22\pi x(2x^2-x^3)dx=2\pi\int_0^2(2x^3=x^4)dx\\ &=2\pi\left(\frac{x^4}{2}+\frac{x^5}{5}\right)\Big|_0^2=2\pi (8-\frac{32}{5})\\ &=\frac{16\pi}{5}\end{align*}\]
我们看到,如果使用切片法来求这个旋转体的体积,会相当麻烦,首先我们要求出函数的反函数(事实上这个函数的反函数很复杂),而且区域的左、右曲线的表达式都不是常数;另外,还需要求出 \(y\) 的最大值。而圆桶法完全避开了这些困难。
例2:求由 \(y=\sqrt{x},y=1,x=0\) 所围成的区域分别绕 \(x\) 轴与绕 \(y\) 轴旋转所得的旋转体的体积。
解:平面区域如图,

我们用切片法求绕 \(x\) 轴旋转的体积,用圆桶法求绕 \(y\) 轴旋转的体积。
(1)绕 \(x\) 轴旋转:
\[V=\int_0^1\pi (1-(\sqrt{x})^2)dx=\pi \left(x-\frac{x^2}{2}\right)\Big|_0^1=\frac{\pi}{2}\]
(2)绕 \(y\) 轴旋转:
\[V=\int_0^12\pi x(1-\sqrt{x})dx=2\pi\left(\frac{x^2}{2}-\frac{2}{5}x^{\frac{5}{2}}\right)\Big|_0^1=\frac{\pi}{5}\]
