有些时候,采用极坐标来计算平面区域的面积会比较方便。我们这一节来导出在极坐标下平面图形的面积的计算公式。
1,极坐标:在平面上,我们称 \(Ox\) 轴为极轴,平面上的一点 \(P\) 可以用极坐标 \(P=(\rho,\theta)\) 表示它的位置。这里 \(\rho\) 为点 \(P\) 到原点的距离,\(\theta\) 为 \(OP\) 与极轴的正向夹角,就是一条射线从极轴出发,逆时针旋转与 \(OP\) 重合所转动的角度。
从极坐标的定义,我们有下列关系
\[\begin{cases}x=\rho \cos\theta\\ y=\rho\sin \theta\end{cases},\qquad\begin{cases}\rho=\sqrt{x^2+y^2}\\ \theta=\begin{cases}\arctan\frac{y}{x},& y>0\\ \arctan\frac{y}{x}+\pi,& y>0\end{cases}\end{cases}\]
2,极坐标系下平面区域的面积:
(1)若区域由 \(\rho=\rho(\theta), \theta_1\le \theta\le \theta_2\) 所围成,则它的面积为 \[A=\frac{1}{2}\int_{\theta_1}^{\theta_2}\rho^2{\theta}d\theta\]
我们来推导这样的结论。我们用 \(\theta=\)常数将区域划分成一个个子区域,
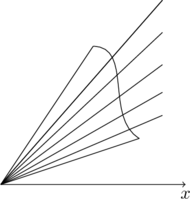
每一个子区域可以用扇形来近似,在子区域 \(\Delta D_i\) 上,任取一个角度 \(\theta_i^*\),\(\rho(\theta)\approx \rho(\theta_i^*)\),所以\(\Delta D_i\) 的面积近似于
\[\Delta A_i\approx \frac{1}{2}\rho^2(\theta_i^*)\Delta \theta_i\]
将所有的小区域的面积加在一起,就是区域面积的近似值。与标准的定积分定义一样,我们将区域划分更细,则近似程度越高,当 \(\Delta \theta\) 接近于 \(0\) 时,近似值的极限就是面积的精确值,即
\[A=\frac{1}{2}\int_{\theta_1}^{\theta_2}\rho^2(\theta)d\theta\]
(2)若区域由曲线 \(\rho_1(\theta), \rho_1(\theta), \theta=\theta_1,\theta=\theta_2\)所围成,其中 \(\rho_1(\theta)\) 为靠近原点的曲线,\(\rho_2(\theta)\) 为远离原点的曲线。则
\[A=\frac{1}{2}\int_{\theta_1}^{\theta_2}(\rho_2^2(\theta)-\rho_1^2(\theta))d\theta\]
例1:计算螺线 \(\rho=a\theta\) 在 \(\theta=0\) 到 \(\theta=2\pi\) 以及极轴所围成的图形的面积。
解:区域的图形为

它的面积为
\[\begin{align*}A&=\int_0^{2\pi}\frac{1}{2}(a\theta)^2d\theta=\frac{1}{6}a^2\theta^3\Big|_0^{2\pi}\\ &=\frac{4}{3}a^2\pi^3\end{align*}\]
例2:计算平面区域位于曲线 \(\rho=s\sin\theta\) 的内部和曲线 \(\rho=1+\sin\theta\) 的外部这一部分的面积。
解:我们先求交点 \[\begin{cases}\rho=3\sin\theta\\ \rho=1+\sin\theta,\end{cases}\] 我们得到 \(2\sin\theta=1\),\(\theta=\frac{\pi}{6},\frac{5\pi}{6}\)。
我们再来看它的图形
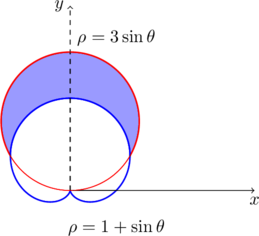
所以面积为远曲线减去近曲线的积分,
\[\begin{align*}A&=\frac{1}{2}\int_{\frac{\pi}{6}}^{\frac{5\pi}{6}}\left((3\sin\theta)^2-(1+\sin\theta)^2\right)d\theta\\ &=\frac{1}{2}\int_{\frac{\pi}{6}}^{\frac{5\pi}{6}}\left(9\sin^2\theta-1-2\sin\theta-\sin^2\theta\right)d\theta \\&=\frac{1}{2}\int_{\frac{\pi}{6}}^{\frac{5\pi}{6}}\left(8\sin^2\theta-1-2\sin\theta\right)d\theta\\ &=\frac{1}{2}\int_{\frac{\pi}{6}}^{\frac{5\pi}{6}}\left(4-4\cos2\theta-1-2\sin\theta\right)d\theta\\ &=\frac{1}{2}\left(3\theta-2\sin2\theta+2\cos\theta\right)\Big|_{\frac{\pi}{6}}^{\frac{5\pi}{6}}\\ &=\pi\end{align*}\]
