我们从曲边梯形的面积导出了定积分的概念,现在我们用定积分来求一般平面图形的面积。
1,曲边梯形的面积:假设曲边梯形的顶为 \(y=f(x)\),底为 \(x\) 轴,那么介于 \(x=a\) 与 \(x=b\) 之间的曲边梯形的面积为
\[A=\int_a^bf(x)dx\]
现在我们利用同样的思想,得到一般平面图形的面积。
2,假如平面图形由 \(y=f(x), y=g(x), x=a, x=b\) 所围成,

则面积为上曲线减去下曲线的积分, \[A=\int_a^b(g(x)-f(x))dx\]
我们来推导这个公式。与定积分定义一样,我们将区间划分成 \(n\) 个小区间,
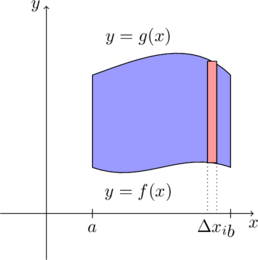
那么在任何一个小区间上,长方形的高为 \(g(x_i^*)-f(x_i^*)\),底边长为 \(\Delta x_i\),第 \(i\) 个长方形的面积为 \((g(x_i^*)-f(x_i^*))\Delta x_i\),将所有这些长方形的面积加起来,就是平面图形面积的近似值;再将区间划分得更细,近似程度越高,当区间的长度趋近于 \(0\) 时,面积的近似值的极限就是平面图形面积的精确值。所以
\[A=\lim_{\Delta x\to 0}\sum_{i=1}^{n}(g(x_i^*)-f(x_i^*))\Delta x_i=\int_a^b(g(x)-f(x))dx\]
3,若平面图形由 \(x=h_1(y), x=h_2(y), y=c, y=d\) 所围成,

跟上面的方法一样,第 \(i\) 个长方形的面积为 \((h_2(y_i^*)-h_1(y_i^*))\Delta y_i\),所以面积为 \[A=\int_c^d(h_2(y)-h_1(y))dy\]
也可以说,用右曲线减去左曲线(关于 \(y\))的积分就是平面图形的面积。
4,如果上、下曲线(或者左、右曲线)在不同区间表达式不同,就需要分成两个或者更多个区间来计算。例如平面区域如图,
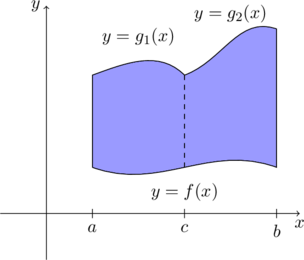
\[A=\int_a^c(g_1(x)-f(x))dx+\int_c^b(g_2(x)-f(x))dx\]
我们来看一些例题。
例1:求由曲线 \(y=x^2,y=2x-x^2\) 所围成的图形的面积。
解:我们先求出曲线的义点,
\[\begin{cases}y=x^2\\ y=2x-x^2\end{cases}\quad\Rightarrow\quad x=0,1\]
所以交点为 \((0,0), (1,1)\)。我们现在画出区域的图形,
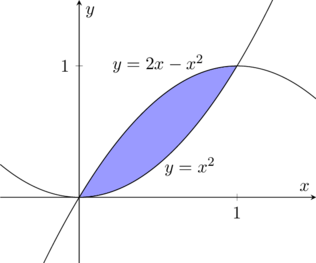
从图形上看,我们知道上曲线是 \(y=2x-x^2\),下曲线是 \(y=x^2\) (如果不画图的话,可以用 \((0,1)\) 区间上任何一点的值代入这两个曲线方程里去,大的那个是上限,小的那个是下限。)所以区域的面积为
\begin{align*}A&=\int_0^1(2x-x^2-x^2)dx=\int_0^1(2x-2x^2)dx\\ &=\left(x^2-\frac{2}{3}x^3\right)\Big|_0^1=\frac{1}{3}\end{align*}
例2:计算曲 \(y=\cos x,y=\sin x, x=0, x=\frac{\pi}{2}\) 所围成图形的面积。
解:我们先画出区域的图形,

我们求出两个曲线的交点, \(\sin x=\cos x\),所以交点为 \(x=\frac{\pi}{4}\),区域要分成两部分,从而面积为
\[\begin{align*}A&=\int_0^{\frac{\pi}{4}}(\cos x-\sin x)dx+\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}(\sin x-\cos x)dx\\ &=(\sin x+\cos x)\Big|_0^{\frac{\pi}{4}}+(-\cos x-\sin x)\Big|_{\frac{\pi}{4}}^{\frac{\pi}{2}}\\ &=2(\sqrt2-1)\end{align*}\]
例3:求由曲线 \(y^2=2x+6,y=x-1\) 所围成的图形的面积。
解:我们先画出函数的图形,
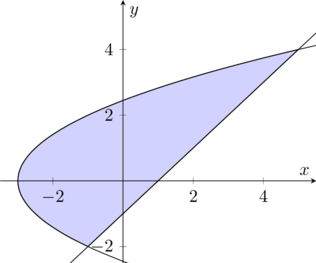
我们来求交点,\begin{cases}y^2=2x+6\\ y=x-1\end{cases} 将第二个方程改写成 \(x=y+1\) 代入第一个方程,我们得到 \[y^2-2y-8=0,\quad y=-2,4\]所以交点为 \((-1,-2),(5,4)\)。
从图形上可以看出,如果以 \(x\) 为积分变量的话,需要将区域分成两部分,来分别求面积,而且被积函数是根式函数。但是如果以 \(y\) 为积分变量,则不需要划分区域,被积函数也比较简单,都是多项式。所以我们以 \(y\) 为积分变量,右曲线是 \(x=y+1\),左曲线是 \(x=\frac{y^2}{2}-3\),所以
\[\begin{align*}A&=\int_{-2}^4\left[y+1-\left(\frac{y^2}{2}-3\right)\right]dy\\ &=\left(\frac{y^2}{2}+4y-\frac{y^3}{6}\right)\Big|_{-2}^4\\ &=18\end{align*}\]
