如果我们从数的一侧(左边或者右边)趋近于这个数,那么所得到的函数的极限就分别为左、右极限,这就是单侧极限的定义。单侧极限的意义在于,左右极限存在且相等,那么函数在该点的极限才存在。
左极限:当 \(x\) 从 \(a\) 的左边越来越接近于 \(a\) 时, 函数 \(f(x)\) 越来越接近于 \(A\),我们就说\(A\) 为函数\(f(x)\) 当 \(x\) 趋近于 \(a\) 左边时的极限,记为 \[\lim_{x\to a^-}f(x)=A\]
同理,我们可以定义函数在 \(a\) 处的右极限。右极限记为 \[\lim_{x\to a^+}f(x)=A\]
对于单侧极限,我们有这样的定理:
定理:函数在一点处的极限存在的充分必要条件是它在这一点处的左、右极限存在且相等。即\[\lim_{x\to a}f(x)=A \Leftrightarrow \lim_{x\to a^-}f(x)=\lim_{x\to a^+}f(x)=A\]
单侧极限通常应用在分段函数中。
例1:设函数 \(f(x)\) 的图形为
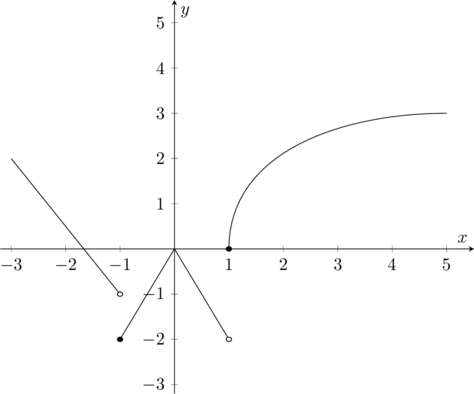
求 \begin{align*}&\lim_{x\to -1^-}f(x),\quad \lim_{x\to -1^+}f(x),\quad\lim_{x\to -1}f(x)\\ &\lim_{x\to 0^-}f(x),\quad\lim_{x\to 0^+}f(x),\quad\lim_{x\to 0}f(x) \\ & \lim_{x\to 1^-}f(x),\quad\lim_{x\to 1^+}f(x),\quad\lim_{x\to 1}f(x)\end{align*}
解,我们可以看到 \[\lim_{x\to -1^-}f(x)=-1,\quad \lim_{x\to -1^+}f(x)=-2\]所以 \(\lim_{x\to -1}f(x)\) 不存在。
在 \(x=0\) 左右, \[\lim_{x\to 0^-}f(x)=0,\quad \lim_{x\to 0^+}f(x)=0\] 所以 \(\lim_{x\to 0}f(x)=0\)。
在 \(x=1\) 左右, \[\lim_{x\to 1^-}f(x)=-1,\quad \lim_{x\to 1^+}f(x)=0\]所以 \(\lim_{x\to 1}f(x)\) 不存在。
例2:设 \[f(x)=\begin{cases}x^2-1,& x<0\\ 0,& x=0\\ x^2+1,& x>0\end{cases},\]求 \(\lim_{x\to0}f(x)\)。
解:因为 \[\lim_{x\to0^-}f(x)=\lim_{x\to0^-}x^2-1=-1,\quad \lim_{x\to0^+}f(x)=\lim_{x\to0^-}x^2+1=1\] 函数在 \(x=0\) 处左、右极限不相等。所以\(\lim_{x\to 0}f(x)\) 不存在。
