极限的直观定义

极限的概念是微积分的基础，我们用直观的方法来定义极限。通过函数的图形、数值、函数表达式等直观的方法定义函数在某一处的极限。

下面的文字部分与视频可能稍有不同，它不是视频的逐字记录。

考察函数 \(f(x)=x^2-x+2\)，这是一个二次函数，我们通过配方法得到它的标准形式：

\[x^2-x+2=(x^2-x)+2=(x-\frac{1}{2})^2+\frac{7}{4}\]所以它的顶点在 \((\frac{1}{2}, \frac{7}{4})\)，由此我们可以画出它的图形

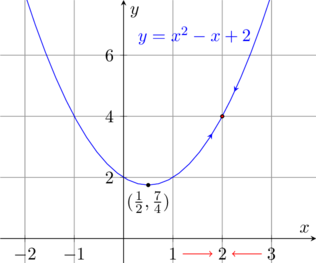
从图形上看，当 \(x\) 越来越趋近于 \(2\) 时，\(y\) 越来越趋近于 \(4\)。所以函数当 \(x\) 趋近于 \(2\) 时的极限为 \(4\)。

我们现在用另一种方法来说明函数在 \(x\) 趋近于 \(2\) 的时候极限是 \(4\)。我们来看当 \(x\) 接近于 \(2\) 的时候函数的值的变化。

\[\begin{array}{l|l}x&f(x)=x^2-x+2\\ \hline\\ 1.8 & 3.44\\ 1.9&3.71\\ 1.95&3.8525\\ 1.99& 3.9701\\ 1.995&3.985025\\ 1.999& 3.997001 \to 4\\ 2.001&4.003001 \to 4\\ 2.005&4.015025\\ 2.01&4.0301\end{array}\]

从这个表我们可以看出，当 \(x\) 越来越接近于 \(2\) 的时候，函数值越来越接近于 \(4\)，所以我们说函数在当 \(x\) 趋近于 \(2\) 的时候的极限为 \(4\)。

所以我们可以给出极限的直观定义如下：

定义1：当 \(x\) 越来越接近于 \(a\) 时，函数 \(f(x)\) 的值越来越接近于 \(A\) ，我们称 \(A\) 为函数 \(f(x)\) 当 \(x\) 趋近于 \(a\) 时的极限，记为 \[\lim_{x\to a }f(x)=A\]或者\[f(x)\to A (x\to a)\]

另外一个稍微严格一点的定义为：

定义1’：若 \(x\) 充分接近 \(a\) 时，函数 \(f(x)\) 的值可以任意接近于 \(A\)，则称\(A\) 为函数 \(f(x)\) 当 \(x\) 趋近于 \(a\) 时的极限，记为 \[\lim_{x\to a }f(x)=A\]或者\[f(x)\to A (x\to a)\]

这里我们要注意的一点是：在极限的定义中，我们并不要求函数 \(f(x)\) 在 \(a\) 点有定义，我们只需要它在这一点的附近有定义即可。也就是说，极限只管这一点附近的情况，对于这一点本身，我们不关心。

另一个我们需要注意的是，极限是一个过程，它是动态的，从定义来看，它是“越来越”，而不是固定在某一点，所以它是一个动态的过程。

我们来看一个例子。

例1：估计极限 \(\lim_{x\to 1}\frac{x-1}{x^2-1}\)。

解：我们知道这个函数在\(x=1\) 时没有定义。但是从我们上面的叙述，我们知道，极限跟函数在一点有没有定义没有关系。

当 \(x\ne 1\) 时，\[\frac{x-1}{x^2-1}=\frac{x-1}{(x-1)(x+1)}=\frac{1}{x+1}\]所以当 \(x\) 接近于 \(1\) 时， \(\frac{1}{x+1}\) 接近于 \(\frac{1}{2}\)，所以我们可以得出\[\lim_{x\to 1}\frac{x-1}{x^2-1}=\frac{1}{2}\]

我们还可以用数值计算来验证这个极限是正确的。

\[\begin{array}{l|l} x& f(x)=\frac{x-1}{x^2-1}\\ \hline \\ 0.9& 0.5263\\ 0.95&0.5128\\ 0.99&0.5025\\ 0.995&0.5013\\ 0.999&0.5003 \to \frac{1}{2}\\ 1.001&0.4998 \to \frac{1}{2}\\ 1.005&0.4988 \end{array}\]