本文离线版本下载:
对坐标的曲线积分的计算方式有很多种,我们所知道或者教材上提到过的就有:直接计算,利用格林公式计算,利用 Stokes 公式,利用积分与路径无关以及全微分求积等等。而且有些方法在不同情况下还有不同的变化。这么多方法,再加上对坐标的曲线积分还需要分方向等等,造成了很多同学感觉对坐标的曲线积分很难的印象。
这一篇文章里我们总结一下求对坐标的曲线积分的方法,以及每种方法的应用情况,这样,我们遇到对坐标的曲线积分时,能够采用针对性的方法来求。
事实上,我们只需要掌握两种方法即可:直接计算法和利用格林公式求积分两种方法。因为能够采用全微分求积或者积分路径无关的方法来求曲线积分的,采用格林公式来求更简单直接。所以我们只总结这两种方法。
对于三维闭曲线上的积分,可以应用 Stokes 公式来求,但它的思想与平面上的格林公式一致,我们只简单介绍一下它的方法。
1,直接计算法:我们根据曲线 \(L\) 的表达式的不同形式,将曲线积分化成定积分来计算。
- 若曲线 \(L\) 是由参数方程 \( x=\phi(t),y=\psi(t)\} \)给出,\(t\) 从 \(\alpha\) 到 \(\beta\),其中 \(t=\alpha\) 对应起点, \(t=\beta\) 对应终点,那么积分 \begin{align*}\int_LP(x,y)dx&+Q(x,y)dy\\&=\int_{\alpha}^{\beta}P(\phi(t),\psi(t))\cdot\phi'(t)dt+Q(\phi(t),\psi(t))\cdot\psi'(t)dt\end{align*}其中 \(x,y\) 都用 \(t\) 表示。这里要注意的是,这里不管 \(\alpha\) 和 \(\beta\) 谁大谁小,起点就是在下限,终点在上限,这一点跟对弧长的曲线积分不同。
- 若曲线 \(L\) 是由参数方程 \(x=\phi(t),y=\psi(t),z=\gamma(t)\}\) 给出,\(t\) 从 \(\alpha\) 到 \(\beta\),其中 \(t=\alpha\) 对应起点, \(t=\beta\) 对应终点,那么积分 \begin{align*}\int_LP(x,y,z)dx&+Q(x,y,z)dy+R(x,y,z)dz\\&=\int_{\alpha}^{\beta}P(\phi(t),\psi(t),\gamma(t))\cdot\phi'(t)dt\\ &\quad+Q(\phi(t),\psi(t),\gamma(t))\cdot\psi'(t)dt\\ &\quad+R(\phi(t),\psi(t),\gamma(t))\cdot\gamma'(t)dt\end{align*}其中 \(x,y,z\) 都用 \(t\) 表示。剩下的部分就是计算定积分了。
- 若曲线是由一个函数 \(y=f(x)\), \(x\) 从 \(a\) 到 \(b\),那么积分 \[\int_LP(x,y)dx+Q(x,y)dy=\int_{a}^{b}P(x,f(x))+Q(x,f(x))\cdot f'(x)dx\]
2,若 \(L\) 是平面曲线,则可以用格林公式来计算。
- 若 \(L\) 是平面闭曲线,且在曲线内部 \(P(x,y), Q(x,y)\) 有一阶连续偏导数,这种情况可以直接应用格林公式;
- 若 \(L\) 是平面闭曲线,但是在曲线内部 \(P(x,y), Q(x,y)\) 有奇点(一阶偏导数不存在或者不连续),这种情况我们通过添加辅助线,将奇点挖掉,然后应用格林公式。最后将辅助线上的积分减去,就得到了原来的曲线积分的值,\begin{align*}\oint_L P(x,y)dx+Q(x,y)dy&=\iint_D\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)dydx\\ &\quad-\oint_{L_1}P(x,y)dx+Q(x,y)dy\end{align*} 这里 \(L\) 取正向, \(L_1\) 都取反向(顺时针方向)。

- 若 \(L\) 是平面开曲线,我们可以通过添加简单的辅助线(为了方便计算),使新的曲线成为一个简单闭曲线,然后应用格林公式,最后减去辅助线上的积分,就得到原曲线积分的值。\begin{align*}\oint_LP(x,y)dx+Q(x,y)dy&=\iint_D\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)dxdy\\ &\quad-\int_{L_1}P(x,y)dx+Q(x,y)dy\end{align*}

3,若 \(L\) 是一个空间闭曲线,则可应用Stokes 公式,将曲线积分化成曲面积分。在曲面的选择上,可以选择比较简单的、容易计算的曲面来进行计算。(因为以 \(L\) 为边界的曲面很多,我们可以选择最简单的曲面。)
理论上来说,空间开曲线也可以通过添加辅助线的方式来应用 Stokes 公式,但一般来说,这样的计算相对繁琐,我们一般不考虑。
4,计算方法选择:现在的问题是在什么情况采取什么方法来求积分?
基本的思想是:(1)闭曲线,基本上采用格林公式或者 Stokes 公式来求,不管内部是不是有奇点;
(2)开曲线:如果曲线简单(例如直线)并且被积函数简单,直接计算;
(3)开曲线:如果曲线复杂,或者被积函数复杂,采用格林公式计算。
现在我们来看如何应用上述的结论。
例1,求积分 \(\int_L(x+y)dx+(y-x)dy\),其中 \(L\) 是抛物线 \(y^2=x\) 从点 \((1,1)\) 到 \((4,2)\) 之间的一段弧。
解:这里,被积函数很简单,曲线也简单,可以用直接方法计算。用 \(y\) 作自变量会更简单一点,不用计算根式函数的导数。
\begin{align*}\int_L(x+y)dx+(y-x)dy&=\int_1^2[(y^2+y)\cdot 2y+(y-y^2)]dy\\ &=\int_1^2(2y^3+y^2+y)dy\\ &=\frac{1}{2}y^4+\frac{1}{3}y^3+\frac{1}{2}y^2\Big|_1^2\\ &=8+\frac{8}{3}+2-\frac{1}{2}-\frac{1}{3}-\frac{1}{2}\\ &=\frac{34}{3}\end{align*}
例2:计算 \(\displaystyle\oint_L\frac{-ydx+xdy}{x^2+y^2}\),其中 \(L\) 是 (1)圆周 \((x-2)^2+y^2=1\);(2)原点在其内部的任一正向闭曲线。
解:(1)曲线为圆心在点 \((2,0)\),半径为 \(1\) 的圆周,在其内部 \(D\) 上 \(P(x,y), Q(x,y)\) 一阶连续可导。所以由格林公式
\begin{align*}\oint_{L}\frac{-ydx+xdy}{x^2+y^2}&=\iint_D\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)dydx\\ &=\iint_D\left(\frac{y^2-x^2}{(x^2+y^2)^2}-\frac{y^2-x^2}{(x^2+y^2)^2}\frac{\partial P}{\partial y}\right)dydx\\ &=\iint_D 0dydx=0\end{align*}
(2)因为被积函数在原点处没有定义,所以原点是被积函数的奇点。我们以原点为心,作一个半径为 \(\epsilon \) 的圆 \(L_{\epsilon}\),那么被积函数在介于 \(L\) 与 \(L_{\epsilon}\) 之间的区域内是一阶连续可导的。
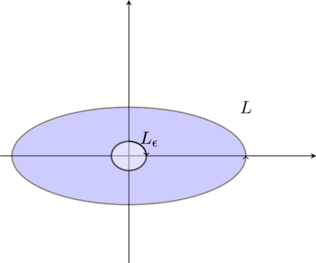
这里 \(L\) 是正向,逆时针,\(L_{\epsilon}\) 是反向,顺时针。介于这两条曲线之间的区域我们记为 \(D\),它的边界为 \(L+L_{\epsilon}\),由格林公式,
\[\oint_L\frac{-ydx+xdy}{x^2+y^2}+\oint_{L_{\epsilon}}\frac{-ydx+xdy}{x^2+y^2}=\iint_D\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)dxdy\]
因为 \[\frac{\partial Q}{\partial x}=\frac{y^2-x^2}{x^2+y^2}, \frac{\partial P}{\partial y}=\frac{y^2-x^2}{x^2+y^2}\]所以 \[\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=0\quad\Rightarrow\quad\iint_D\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)dxdy=0\]
所以我们得到 \[\oint_L\frac{-ydx+xdy}{x^2+y^2}=-\oint_{L_{\epsilon}}\frac{-ydx+xdy}{x^2+y^2}\]
因为 \(L_{\epsilon}\) 可用参数方程表示为 \(x=\epsilon\cos t, y=\epsilon \sin t\),顺时针方向,所以 \(t\) 是从 \(2\pi\) 到 \(0\),
\begin{align*}-\oint_{L_{\epsilon}}\frac{-ydx+xdy}{x^2+y^2}&= -\int_{2\pi}^0\left(\frac{-\epsilon\sin t \epsilon (-\sin t)+\epsilon\cos t\epsilon\cos t}{\epsilon^2}\right)dt\\ &=\int_0^{2\pi}\frac{\epsilon^2\sin^2t+\epsilon^2\cos^2t}{\epsilon^2}dt=\int_0^{2\pi}dt=2\pi\end{align*}
所以 \[\oint_L\frac{-ydx+xdy}{x^2+y^2}=2\pi\]
例3:计算 \(\int_L(2xy^3-y^2\cos x)dx+(1-2y\sin x+3x^2y^2)dy\),其中 \(L\) 是抛物线 \(2x=\pi y^2\) 上从点 \((0,0)\) 到 \((\frac{\pi}{2}, 1)\) 之间的一段。
解:积分的曲线如图:

如果直接计算,这个积分基本上是求不出来的,但是利用格林公式,计算就变得很简单。但是这个曲线不是闭曲线,我们需要添加辅助线来将它变成闭曲线。

我们看到整个闭曲线的方向是顺时针方向,它是逆向的,所以
\begin{align*}\left(\int_L+\int_{L_1}+\int_{L_2}\right)P(x,y)dx&+Q(x,y)dy=-\iint_D\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)dxdy\end{align*}
我们先来计算右边的积分。因为
\begin{align*}&\frac{\partial Q}{\partial x}=\frac{\partial}{\partial x}(1-2y\sin x+3x^2y^2)=-2y\cos x+6xy^2,\\ &\frac{\partial P}{\partial y}=\frac{\partial}{\partial x}(2xy^3-y^2\cos x)=6xy^2-2y\cos x\end{align*}
所以 \[\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=0,\qquad \iint_D\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)dxdy=0\]
那么 \[\int_LPdx+Qdy=-\int_{L_1}Pdx+Qdy-\int_{L_2}Pdx+Qdy\]
在 \(L_1\) 上,\(x=\frac{\pi}{2}, dx=0\), \(y\) 从 \(1\) 到 \(0\)。所以
\begin{align*}-\int_{L_1}Pdx+Qdy&=-\int_1^0Q(x,y)dy\\ &=-\int_1^0\left(1-2y+3\left(\frac{\pi}{2}\right)^2y^2\right)dy\\ &=\int_0^1\left(1-2y+3\left(\frac{\pi}{2}\right)^2y^2\right)dy\\ &=y-y^2+\frac{\pi^2}{4}y^3\Big|_0^1=\frac{\pi^2}{4}\end{align*}
在 \(L_2\) 上, \(y=0,dy=0\),\(x\) 从 \(\frac{\pi}{2}\) 到 \(0\)。所以
\[-\int_{L_2}Pdx+Qdy=-\int_{L_2}Pdx=-\int_{L_2}0dx=0\]
所以
\[\int_L(2xy^3-y^2\cos x)dx+(1-2y\sin x+3x^2y^2)dy=\frac{\pi^2}{4}\]
最后是一些习题供同学们练习。
1,设 (C) 是从 ((1,0)) 到 ((0,1)) 再到((-1,0)) 的折线,求下列曲线积分
(1)\(\displaystyle\int_C2xydx+x^2dy\);(2)\(\displaystyle\int_Cye^{xy}dx+xe^{xy}dy\);(3)\(\displaystyle\int_Cx^{2/3}dx+e^{7y}dy\)。
2,求曲线积分 \(\displaystyle\int_C(x^2+y)dx+xdy\),其中 \(C\) 是曲线 \(y=9-x^2\) 从 \((-3,0)\) 到 \((3,0)\) 的一段。
3,求积分 \(\displaystyle\int_Cxydx+(e^y+x^2)dy\),其中 (C) 是由 \(y=x^2+4x+4\) 与 (y=4-x^2) 围成的区域的正向边界。
4,计算积分 \(\int_C\frac{-y}{x^2+y^2}dx+\frac{x}{x^2+y^2}dy\),其中 \(C\) 为(1)任意一条原点在其内部的正向闭曲线;(2)任意原点在其外部的正向闭曲线;(3)曲线 \(y=\frac{1}{4}x^2+1\) 从点 \((-2,2)\) 到 \((2,2)\) 之间的一段;(4)曲线 \(y=x^2-2\) 从点 \((-2,2)\) 到 \(2,2\) 之间的一段。
5,求积分 \(\displaystyle\oint_C\frac{4x-y}{4x^2+y^2}dx+\frac{x+y}{4x^2+y^2}dy\),其中 \(C\) 为 \(x^2+y^2=2\), 逆时针方向。
答案:1(1)\(\quad 0\quad \)(2)\(\quad 0\quad\)(3)\(\quad\frac{6}{5}\)
2\(\quad 18\quad\) 3 \(\quad-\frac{8}{3}\quad \)
4 (1)\(\quad2\pi\quad \)(2)\(\quad0\quad\)(3)\(\quad-\frac{\pi}{2}\quad\)(4)\(\quad \frac{3\pi}{2}\)
5 \(\quad\pi\quad\)

发表回复