求旋转体的体积是定积分的另一个应用。旋转体的体积求法主要有切片法与圆桶法,这一节我们讲述切片法求旋转体的体积。
1,考虑由 \(y=f(x), x=a, x=b \) 以及 \(x\) 轴所围成的平面区域,绕 \(x\) 轴旋转,求该旋转体的体积。
与定积分定义一样,我们将区域 \([a,b]\) 划分成很多个子区间,在每一个子区间上,旋转体近似于圆柱体,

我们取子区间上任意一点的函数值作为圆柱体的半径,用这个圆柱体的体积近似小旋转体的体积,然后将所有这些小圆柱体的体积相加,得到旋转体体积的近似值。当每一个子区间的长度趋近于 \(0\) 时,这个近似值的极限就是旋转体体积的精确值。
区间\((x_{i-1},x_i)\) 上的圆柱体的体积近似于 \(\Delta V_i\approx \pi f^2(x_i^*)\Delta x_i\),其中 \(x_i^*\) 是 \((x_{i-1},x_i)\) 内任意一点。所以整个旋转体的体积
\[V=\sum_{i=1}^n\pi \Delta V_i\approx\sum_{i=1}^n\pi f^2(x_i^*)\Delta x_i\]
子区间的长度趋近于 \(0\) 时,上式的极限就是旋转体体积的精确值。即
\[V=\lim_{\Delta x\to 0}\sum_{i=1}^nf^2(x_i^*)\Delta x_i\]
这又是和式的极限,就是定积分,所以
\[V=\int_a^b\pi f^2(x)dx\]
我们可以相像旋转体是一个胡萝卜,我们将胡萝卜切成一个个薄片,每一个薄片差不多是一个圆柱体,我们可以用它的一个截面的半径作为整个圆柱体的半径,就可以求出这个薄片的体积的体积的近似值,将所有薄片的体积加起来,就是整个胡萝卜体积的近似值。薄版越薄,近似程度越高。
所以我们称这种方法为切片法,就是相当于将旋转体切成一个个小薄片,每一个薄片用圆柱体近似,加起来再求极限,就是旋转体的体积。
2,同理,若平面区域是由 \(x=h(y), y=c,y=d\) 以及 \(y\) 轴所围成,

则它绕 \(y\) 轴旋转所得的体积为
\[A=\int_c^dh(y)dy\]
例1:求由曲线 \(y=\sqrt{x}, x=1,y=0\) 所围成的图形绕 \(x\) 轴旋所得的旋转体的体积。
解:平面区域如图:
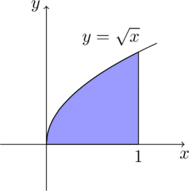
体积为 \[A=\int_0^1\pi (\sqrt{x})^2dx=\int_0^1\pi xdx=\frac{\pi}{2}x^2\Big|_0^1=\frac{\pi}{2}\]
例2:求由曲线 \(y=x^3, y=8,x=0\) 所围成的图形绕 \(y\) 轴旋转所得的旋转体的体积。
解:平面区域如图
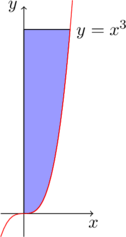
旋转体的体积为
\[V=\int_0^8\pi x^2dy=\int_0^8\pi(\sqrt[3]{y})^2dy=\frac{3\pi}{5}y^{\frac{5}{3}}\Big|_0^8=\frac{96\pi}{5}\]
3,若平面区域由 \(y=f_1(x),y=f_2(x), x=a,x=b\) 所围成,

则区域绕 \(x\) 轴旋转所得的体积为
\[V=\int_a^b\pi(f_2^2(x)-f_1^2(x))dx\]
4,若平面区域由 \(x=h_1(x),x=h_2(x), y=c,y=d\) 所围成,

则平面区域绕 \(y\) 轴旋转所得的体积为
\[V=\int_c^d\pi(h_2^2(y)-h_1^2(y))dy\]
例3:求由 \(y=\sqrt{x},x=1,y=0\) 绕 \(y\) 轴旋转所得的体积。
解:这是绕 \(y\) 轴旋转的,要注意用右曲线旋转所得减去左曲线旋转所得的体积。区域的图形如例1,右曲线为 \(x=1\),左曲线为 \(x=y^2\),所以
\[\int_0^1\pi (1-(y^2)^2)dy=\pi\int_0^1(1-y^4)dy=\pi\left(y-\frac{y^5}{5}\right)\Big|_0^1=\frac{4\pi}{5}\]
