如果在任何一点 \(x\)处,立体的截面积已知为 \(A(x)\),则该立体的体积为 \[V=\int_a^bA(x)dx\]
跟之前一样,我们将区间 \([a,b]\) 划分成 \(n\) 个小区间,在每个小区间上,立体可以近似于一个柱体,底面积为 \(A(x_i^*\) ,高为 \(\Delta x_i\),所以这个小的立体的体积近似于\[\Delta V_i\approx A(x_i^*)\Delta x_i\]
整个立体的体积近似于\[V=\sum_{i=1}^n\Delta V_i\approx\sum_{i=1}^n A(x_i^*)\Delta x_i\]
当每个子区间的长度趋近于 \(0\) 时,上式的极限就是立体体积的精确值,即
\[V=\lim_{\Delta x\to 0}\sum_{i=1}^n A(x_i^*)\Delta x_i\]
这是和式的极限,所以它可以用定积分表示,
\[V=\int_a^bA(x)dx\]
例1:求底边为单位圆,每个平行截面为等边三角形的立体的体积。
解:题目给出了平行截面的面积信息,所以我们可以先求出平行截面的面积,然后利用上面的公式求出体积。
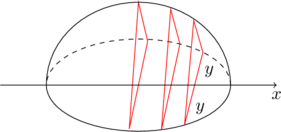
因为底边是单位圆,我们假设它的圆心在原点。所以对于任何 \(x\),\(y=\pm\sqrt{1-x^2}\),所以三角形的底边与侧边都是 \(2\sqrt{1-x^2}\),因为是等边三角形,所以底角为\(\frac{\pi}{3}\),高为 \(\sqrt{3}y=\sqrt3\sqrt{1-x^2}\)。
所以平行截面的面积为 \(A(x)=\sqrt3(1-x^2)\)。根据之前的推导,我们得到立体的体积为
\[\int_{-1}^1\sqrt3(1-x^2)dx=\sqrt{3}\left(x-\frac{x^3}{3}\right)\Big|_{-1}^1=\frac{4}{\sqrt{3}}\]
例2:求底部边长为 \(L\) 的正方形,高为 \(h\) 的金字塔的体积。
解:我们用水平的平面去截金字塔,那么每个截面都是正方形,我们利用相似三角形就可以求出每个截面的边长。

我们取从顶部向下,金字塔的高的延长线为 \(x\) 轴。在点 \(x\) 处,截面为正方形,我们假设它的边长为 \(s\),这个边长正好是小红色三角形的底边长。利用相似三角形,小红色三角形与大红色三角形相似,所以我们有比例关系
\[\frac{s}{L}=\frac{x}{h},\quad s=\frac{Lx}{h}\]
所以截面的面积为 \[A(x)=\frac{L^2x^2}{h^2}\]
从而金字塔的体积为 \(\int_0^h\frac{L^2x^2}{h^2}dx=\frac{L^2x^3}{3h^2}\Big|_0^h=\frac{L^2h}{3}\)
也就是说,金字塔的体积为: \(V=\frac{1}{3}\) 底面积 \(\times\) 高。
