留数定理也叫残数定理,它是联系罗朗级数与柯西积分公式的一条重要定理。这个定理也有很多的应用,这一节我们叙述并证明这个定理。
1,留数(残数,residue):设 \(z=a\) 是 \(f(z)\) 的孤立奇点,则 \(f(z)\) 在 \(a\) 处的留数为
\[\text{Res}(f(z),a)=\frac{1}{2\pi i}\int_{|z-a|=\rho}f(z)dz\]
它的值可以用函数的罗朗级数的系数来计算。
2,留数的值:设 \(\displaystyle f(z)=\sum_{n=1}^{\infty}c_{-n}(z-a)^{-n}+\sum_{n=0}^{\infty}c_{n}(z-a)^{n}\),则
\[\text{Res}(f(z),a)=c_{-1}\]
证明:当 \(n\ne 1\) 时,由解析函数的高阶求导公式,
\[\frac{1}{2\pi i}\int_{|z-a|=\rho}\frac{c_{-n}}{(z-a)^n}dz=2\pi i\frac{(c_{-n})^{(n-1)}}{(n-1)!}\]
注意分子是求 \(n-1\) 阶导数,因为 \(c_{-n}\) 是常数,所以求导就为 \(0\)。
当 \(n=0,1,\cdots\) 时,
\[\frac{1}{2\pi i}\int_{|z-a|=\rho}c_{n}(z-a)^ndz=0\]
这是因为被积函数是解析函数,由柯西积分定理,上面的积分为 \(0\)。\(n=1\) 时,由柯西积分公式,
\[\frac{1}{2\pi i}\int_{|z-a|=\rho}\frac{c_{-1}}{z-a}dz=c_{-1}\]
所以\[\text{Res}(f(z),a)=c_{-1}\]
3,留数定理:若 \(f(z)\) 在区域 \(D\) 内除去 \(z_1,z_2,\cdots,z_m\) 外解析, \(f(z)\) 在 \(\bar{D}=D+\partial D\) 内除去 \(z_1,z_2,\cdots,z_m\) 外连续,则
\[\int_{\partial D}f(z)dz=2\pi i\sum_{k=1}^m\text{Res}(f(z),z_i)\]
就是把所有这些孤立奇点的留数加起来再乘以 \(2\pi i\)。
证明:我们就两个奇点的情形证明这个定理,其余的情形类似。设 \(z_1,z_2\) 是区域内两个孤立奇点,应用复连通区域的柯西积分定理,
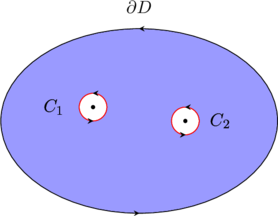
我们有
\begin{align*}\int_{\partial D}f(z)dz&=\int_{C_1}f(z)dz+\int_{C_2}f(z)dz\\ &=\text{Res}(f,z_1)+\text{Res}(f,z_2)\end{align*}
所以可以利用函数的罗朗展开式来计算留数。事实上,我们只需要知道罗朗展开式里的 \(c_{-1}\) 即可,而不需要知道完整的展开式。
例1,求积分 \(\displaystyle\int_{|z|=1}\frac{1}{\sin z}\)。
解:因为
\begin{align*}\frac{1}{\sin z}&=\frac{1}{z-\frac{1}{3!}z^3+\frac{1}{5!}z^5+\cdots}\\ &=\frac{1}{z}\cdot\frac{1}{1-(\frac{1}{3!}z^2-\frac{1}{5!}z^4+\cdots)}\\ &=\frac{1}{z}\left(1+(\frac{1}{3!}z^2-\frac{1}{5!}z^4+\cdots)+(\frac{1}{3!}z^2-\frac{1}{5!}z^4+\cdots)^2+\cdots\right)\\ &=\frac{1}{z}+\frac{z}{3!}+\cdots\end{align*}
所以 \(c_{-1}\),也就是 \(\text{Res}(\frac{a}{\sin z}, 0)=1\)。这里我们将分母括号里面的部分看成一个整体,那么分母就是几何级数的和函数。
从而 \[\int_{|z|=1}\frac{1}{\sin z}dz=2\pi i\text{Res}(\frac{1}{\sin z}, 0)=2\pi i\]
