我们求解数学物理方程时,需要相应的定解条件,主要是初始条件与边界条件。初始条件应该与边界条件相容,也就是在函数相交的地方,函数值应该是一致的。
我们先来看热传导方程的第一边值问题:
\begin{cases}u_t=c^2u_{xx}, &t>0, 0<x<L\\ u(0,t)=\phi(t), u(L,t)=\psi(t),& t>0\\ u(x,0)=g(x),&0<x<L\end{cases}
我们考虑的是方程的古典解,也就是说在方程里出现的各阶导数都是存在而且连续可微的。那么就是说,这个方程的解在区域 \(t>0, 0<x<L\) 上连续可微。
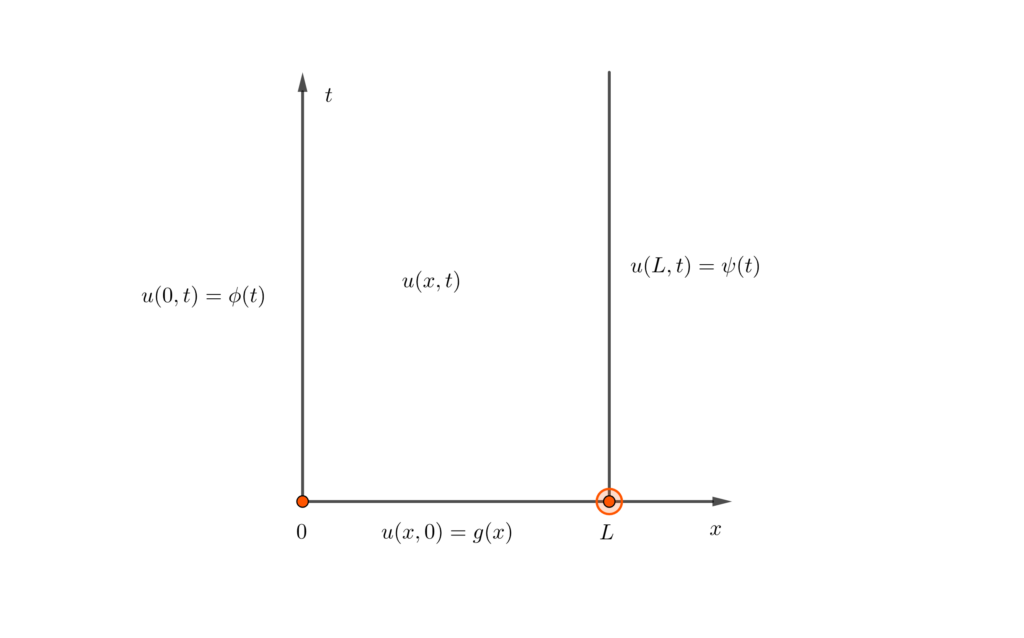
我们看到,在交点 \(t=0,x=0\) 处,\(\phi(t), g(x)\) 的值应该是一样的,它们都等于 \(u(0,0)\)。所以 \(\phi(0)=g(0)\)。同样,在 \(t=0, x=L\) 处,\(\psi(t), g(x)\) 的值也一样,它们都等于 \(u(L,0)\)。所以,\(\psi(0)=g(L)\)。
这就是初边值条件的相容性条件。
2,我们来看一个第二边值问题的相容性条件,考虑初边值问题
\begin{cases}u_t=c^2u_{xx}, &t>0, 0<x<L\\ u_x(0,t)=\phi(t), u_x(L,t)=\psi(t),& t>0\\ u(x,0)=g(x),&0<x<L\end{cases}
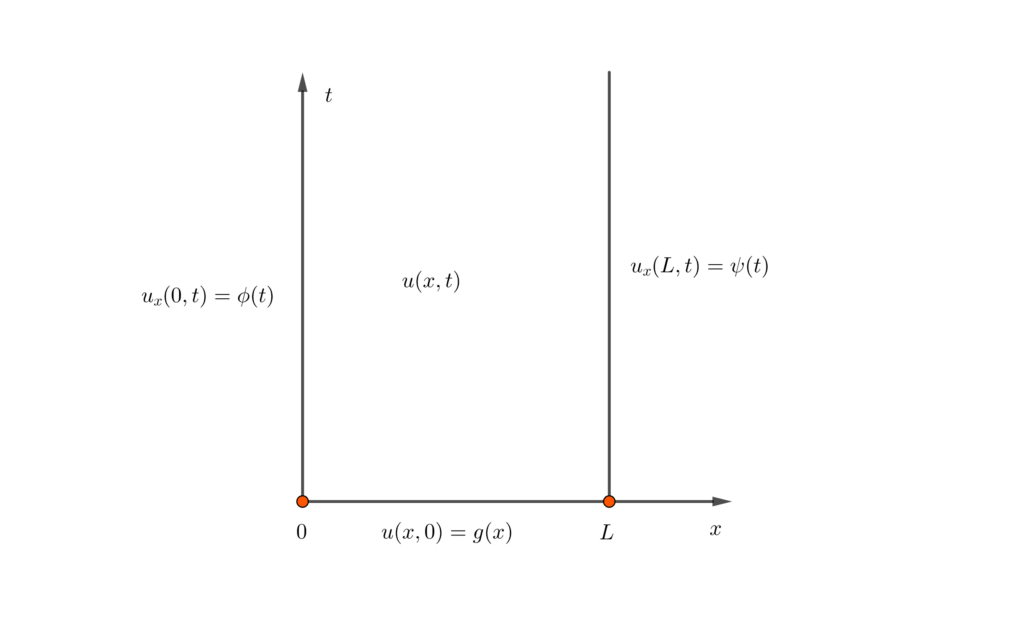
那么在 \((0,0)\) 处,\(u_x(0,0)=\phi(0)\) ,它应该等于 \(g'(0)\),也就是 \(\phi(0)=g'(0)\),它们都等于 \(u_x(0,0)\)。同样的,在 \((L,0)\) 处, \(\psi(0)=g'(L)\),它们都等于 \(u_x(L,0)\)。这就是第二边值问题的相容性条件。
3, 波动方程的相容性条件。波动方程的时间导数是二阶的,所以初始条件比热传导方程多了一个。我们来看第一边值问题:
\begin{cases}u_{tt}=c^2u_{xx}, &t>0, 0<x<L\\ u_x(0,t)=\phi(t), u_x(L,t)=\psi(t),& t>0\\ u(x,0)=g(x), u_t(x,0)=h(x)&0<x<L\end{cases}

在 \((0,0)\) 点处,函数值 \(u(0,0)=\phi(0)=g(0)\),关于时间的导数 \(u_t(0,0)=\phi'(t)=h(0)\);在 \((L,t)\) 点处,函数值 \(u(L,0)=\psi(0)=g(L)\),关于时间的导数 \(u_t(L,t)=\psi'(0)=h(L)\)。所以
\[\phi(0)=g(0),\quad \phi'(t)=h(0),\quad \psi(0)=g(L),\quad u_t(L,t)=\psi'(0)=h(L)\]
