解析函数的一个特点是它们的零点是孤立的,也就是说,在一个零点的附近没有别的零点。另外,若两个解析函数在区域内的某个数列上的值相等,则它们在整个区域上的值相等,这就是解析函数的唯一性。
现在我们来证明这两个定理。
1,定理(解析函数零点的孤立性):若 \(f(z)\) 在区域 \(D\) 内解析, \(z_0\in D\) 为 \(f(z)\) 的零点,则 \(f(z)\) 在 \(z_0\) 的某个邻域内没有其它零点,除非 \(f(z)\) 在 \(D\) 内恒等于 \(0\)。
证明:因为 \(f(z)\) 在 \(D\) 上解析,所以 \(f(z)\) 在 \(z_0\) 处可展开成泰勒级数
\begin{align*}f(z)=a_0+a_1(z-z_0)+a_2(z-z_0)^2+\cdots+a_n(z-z_0)^n+\cdots\\ &=\sum_{n=0}^{\infty}a_n(z-z_0)^n\end{align*}
因为 \(f(z_0)=0\), 所以 \(a_0=0\),现在有两种情况:
(1)\(a_0=a_1=\cdots=a_n=\cdots\),即所有的泰勒系数都为 \(0\),这时候 \(f(z)=0\);
(2)\(a_0=a_1=\cdots=a_{m-1}=0, a_m\ne 0\),这时候称 \(z_0\) 为 \(f(z)\) 的 \(m\) 级零点,所以
\begin{align*}f(z)&=a_m(z-z_0)^m+a_{m+1}(z-z_0)^{m+1}+\cdots\\ &=(z-z_0)^m\sum_{k=0}^{\infty}a_{m+k}(z-z_0)^k\\ &=(z-z_0)^mg(z)\end{align*}
其中 \(g(z)\) 在 \(D\) 上解析且 \(g(z_0)=a_m\ne 0\)。所以在 \(z_0\) 的一个小邻域里,\(g(z)\ne 0\),也就是说,存在 \(\epsilon>0\),使得当 \(0<|z-z_0|<\epsilon\) 时,\(g(z)\ne 0\),从而当 \(0<|z-z_0|<\epsilon\) 时,\(f(z)=(z-z_0)^mg(z)\ne 0\)。也就是说,在 \(z_0\) 的这个去心邻域内,函数 \(f(z)\) 不为 \(0\)。证毕。
2,推论:若函数 \(f(z)\) 在圆盘 \(|z-z_0|<R\) 上解析且有一系列零点 \(\{z_n\}\) 收敛于 \(z_0\),则 \(f(z)\) 在此圆盘上恒等于 \(0\)。
证明:因为 \(z_0\) 是一个非孤立的零点,所以由上述定理,只能是函数恒等于 \(0\)。
3,定理(解析函数的唯一性):设函数 \(f_1(z)\) 和 \(f_2(z)\) 都在 \(D\) 上解析,若在 \(D\) 有一系列点列 \(\{z_n\}\),使得 \(f_1(z_n)=f_2(z_n)\),则在 \(D\) 内 \(f_1(z)=f_2(z)\)。
证明:我们设 \(f(z)=f_1(z)-f_2(z)\),则只需要证明 \(f(z)\) 在 \(D\) 上恒等于零就可以了。
我们利用所谓的“圆链法”来证明这个结论。设 \(\{z_n\}\) 收敛于 \(z_0\)。若 \(D\) 是以 \(z_0\) 为心的圆盘,那么由上面的推论,就可以直接得到结论。
现在设 \(z’\) 为 \(D\) 内任意一点,我们证明 \(f(z’)=0\)。用 \(D\) 的一条折线将 \(z_0\) 与 \(z’\) 连接起来。假设这条折线与 \(D\) 的边界的距离为 \(\rho\)(折线上点到边界的距离的最小值),在折线上选取一系列的点 \(a_0=z_0, a_1,a_1,\cdots,a_{n-1}, a_n=z’\),使得两点之间的距离为 \(R<\rho\)。以这些点为圆心,作半径为 \(r\) 的圆 \(R<r<\rho\) 的一系列圆,
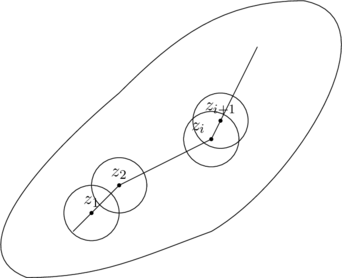
因为 \(z_0\) 是聚点,所以在圆 \(K_1: |z-z_0|<r\) 内\(f(z)=0\),那么在圆 \(K_2:|z-z_1|<R\) 与 \(K_1\) 相交的部分,函数全部为 \(0\)。而 \(z_1\in K_1\),所以 \(z_1\) 是一系列零点的聚点,所以在 \(K_2\) 内函数恒等于 \(0\)。
这样继续下去,直到含有最后一个圆 \(K_n:|z-z’|<r\),在这个圆内,\(f(z)=0\),所以 \(f(z’)=0\)。因为 \(z’\) 是 \(D\) 内任意一点,我们得到在 \(D\) 内,\(f(z)=0\)也就是 \(f_1(z)=f_2(z)\)。证毕。
