每一个复数不光可以用平面上的点表示,还可以与单位球面上的点作一一对应,这种对应关系就是复数的球面表示。这样的球面叫做复球面。所有的平面上的复数加上一个数无穷大 \(\infty\) 组成了扩充复平面。
笔记下载:复球面与扩充复平面
1,复球面:我们用这样的方式将单位球面 \(x^2+y^2+u^2=1\) 上的点与复数对应起来:将单位球面上的北极点 \((0,0,1)\) 与球面上一点 \((x,y,u)\) 连接成一条直线,这条直线与复平面的交点为 \((x’,y’)\),则复数 \(z=x’+iy’\) 就与球面上的点 \((x,y,u)\) 成了一一对应。
我们称 \((x,y,u)\) 为复数 \(z=x’+iy’\) 的球面表示。这个单位球面我们称之为复球面,或者黎曼球面。
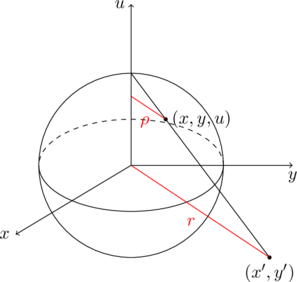
用相似三角形的关系式,
\[\frac{x’}{x}=\frac{y’}{y}=\frac{r}{\rho}=\frac{1}{1-u}\]
我们可以得到这个一一对应的具体表达式为
\[x’=\frac{x}{1-u}, y’=\frac{y}{1-u}\]
所以 \[z=x’+iy’=\frac{x}{1-u}+\frac{y}{1-u}i=\frac{x+iy}{1-u}\]
2,无穷大:我们将球面的北极 \((0,0,1)\) 对应于无穷远点 \(\infty\),这个点也称为无穷大,或者简称为无穷。
3,扩充复平面:我们将复平面加上无穷大,就称为扩充复平面。也就是
\[\mathbb{C}^*=\mathbb{C}\cup \infty\]
4,球极射影是一一对应的,因为
\[z\bar{z}=\frac{x+iy}{1-u}\cdot\frac{x-iy}{1-u}=\frac{x^2+y^2}{(1-u)^2}=\frac{1-u^2}{(1-u)^2}\frac{1+u}{1-u}\ne 0\]
5,注意,扩充复平面的无穷大无正、负之分。但是约定 \(|\infty|=+\infty\)。
6,无穷大的运算:
(1)\(a+\infty=\infty\);
(2)\(a-\infty=\infty-a=\infty\):
(3)\(a\cdot\infty=\infty\cdot a=\infty,\quad a\ne 0\);
(4)\(\frac{a}{\infty}=0, \frac{\infty}{a}=\infty, \quad a\ne \infty\);
(5)\(\frac{a}{0}=\infty\)。
