空间上的闭曲线的积分,可以用曲面积分来计算,这是 Stokes 公式的结论。这一节,我们利用 Stokes 公式来计算空间曲线积分。
我们先回顾一下 Stokes 公式
1,定理(Stokes 公式):设 \(S\) 为有向曲面,\(L\) 为其正向边界,\(P,Q,R\) 在 \(S\) 及其边界上有一阶连续偏导数,则
\[\oint_L\vec{F}\cdot d\vec{r}=\iint_S\text{curl}\vec{F}\cdot\vec{n}dS\]
或者写成坐标的形式
\[\oint_LPdx+Qdy+Rdz=\iint_S\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)dydz+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)dzdx+\left(\frac{\partial Q}{\partial x}-\frac{\partial Q}{\partial z}\right)dxdy\]
我们来看例题。
例1:求曲线积分 \(\oint_L-y^3dx+x^3dy-z^3dz\),其中 \(L\) 是柱面 \(x^2+y^2=1\) 与平面 \(2x+2y+z=3\) 的交线,其投影曲线为逆逆时针方向。
解:从题意我们知道,\(L\) 是曲面 \(2x+2y+z=3\) 的边界,
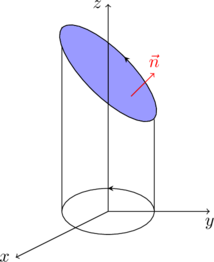
曲线的投影曲线为逆时针方向,所以我们看到,曲面的法向量朝上(\(z\) 分量为正)。因为 \(S\) 可以表示为 \(S: z=3-2x-2y, x^2+y^2\le 1\),所以
\[\vec{n}dS=(-g_x,-g_y,1)dxdy=(2,2,1)dxdy\]
\(\vec{F}=(-y^3,x^3,-z^3)\),它的旋度
\[\text{curl}\vec{F}=\nabla\times \vec{F}=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\ \frac{\partial}{\partial x}& \frac{\partial}{\partial y}&\frac{\partial}{\partial z}\\ -y^3&x^3&-z^3\end{vmatrix}=3x^2+3y^2\vec{k}\]
所以
\[\begin{align*}\oint_L\vec{F}\cdot d\vec{r}&=\oint_L-y^3dx+x^3dy-z^3dz\\ &=\iint_S(0,0,3x^2+3y^2)\cdot(2,2,1)dxdy\\ &=\iint_{x^2+y^2\le 1}(3x^2+3y^2)dxdy\\ &=\int_0^{2\pi}\int_0^13r^2\cdot rdrd\theta\\ &=\int_0^{2\pi}\frac{3}{4}r^4\Big|_0^1d\theta=\frac{3}{4}\theta\Big|_0^{2\pi}\\ &=\frac{3\pi}{2}\end{align*}\]
当然,我们也可以直接用公式
\[\oint_LPdx+Qdy+Rdz=\iint_S\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)dydz+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)dzdx+\left(\frac{\partial Q}{\partial x}-\frac{\partial Q}{\partial z}\right)dxdy\]
来计算,结果是一样的。
