我们还是可以利用向量的点积与叉积来推导直线 之间以及平面之间的距离。
1,两直线之间的距离。假设直线 \(l_1\) 过点\(P_1\) 且有方向向量 \(\vec{s}_1\),直线 \(l_2\) 过点 \(P_2\) 且有方向向量 \(\vec{s_2}\),那我们知道这两条直线的距离就是连接这两条直线且同时垂直于这两条直线的线段的长度。那么这条线段同时垂直于两个向量的方向向量。我们一般不知道这条线段与这两条直线 的交点在什么地方,但是从图形上看,
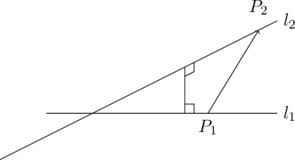
这两条直线之间的距离就是向量 \(\vec{P_1P_2}\) 在向量 \(\vec{s}_1\times\vec{s}_2\) 上的投影的长度,这是因为 \(\vec{s}_1\times\vec{s}_2\) 即垂直于 \(\vec{s}_1\),又垂直于 \(\vec{s}_2\)。所以\[d=|\text{Proj}_{\vec{s}_1\times\vec{s}_2}\vec{P_1P_2}|=\frac{|(\vec{s}_1\times\vec{s}_2)\cdot\vec{P_1P_2}|}{|\vec{s}_1\times\vec{s}_2|}\]
例1:求两直线 \(\frac{x-1}{1}=\frac{y-1}{6}=\frac{z}{2}\) 和 \(\frac{x-1}{2}=\frac{y-5}{15}=\frac{z+2}{6}\) 之间的距离。
解:我们知道第一条直线过点 \(P_1(1,1,0)\),方向向量为 \(\vec{s}_1=(1,6,2)\);第二条直线过点 \(P_2(1,5,-2)\),方向向量为 \(\vec{s}_2=(2,15,6)\)。所以 \(\vec{P_1P_2}=(0,4,-2)\),
\[\vec{s}_1\times\vec{s}_2)=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\ 1&6&2\\2&15&6\end{vmatrix}=6\vec{i}-2\vec{j}+3\vec{k}=(6,-2,3)\]
从而我们得到 \[d=\frac{|(\vec{s}_1\times\vec{s}_2)\cdot\vec{P_1P_2}|}{|\vec{s}_1\times\vec{s}_2|}=\frac{|0+(-8)+(-6)|}{\sqrt{36+4+9}}=\frac{14}{7}=2\]
2,两平面的距离。如果两个平面 不平行,则这两个平面必定相交,所以距离为 \(0\)。现设两个相互平行的平面方程分别为 \[\Sigma_1: A_x+B_1y+C_1z=\tilde{D}_1,\quad \Sigma_2:A_2x+B_2y+C_2z=\tilde{D}_2\]则通过简单的变换,两个平面分别可以写成 \[\Sigma_+1:Ax+By+Cz=D_1,\quad \Sigma_2:Ax+By+Cz=D_2\]利用点到平面 的距离公式, \(\Sigma_2\) 上的任意一点 \((x,y,z)\) 到平面 \(\Sigma_1\) 上的距离为 \[d=\frac{|Ax+By+Cz-D_1|}{\sqrt{A^2+B^2+C^2}}\]又因为 \((x,y,z)\) 在平面 \(\Sigma_2\) 上, 所以 \(Ax+By+Cz=D_2\)从而我们得到两平行平面的的距离为 \[d=\frac{|D_2-D_1|}{\sqrt{A^2+B^2+C^2}}\]
这里我们需要注意一下,这两个平面的方程,各个变量的系数应当变成一样,才可以应用这个公式 。我们来看例题。
例2:求两平面 \(10x+2y-2z=5\) 和 \(5x+y-z=1\) 的距离。
解:我们将第一个平面的方程改写为 \(5x+y-z=\frqac{5}{2}\),那么这两个平面的距离为\[d=\frac{|1-\frac{5}{2}|}{\sqrt{25+1+1}}=\frac{\frac{3}{2}}{\sqrt{27}}=\frac{1}{2\sqrt3}\]
