高斯公式是曲面积分的基本定理,它将闭曲面上的曲面积分与闭曲面内部的三重积分联系起来了,类似于一元微积分的牛顿-莱不尼兹公式。
1,定理(高斯公式,散度公式):设 \(S\) 空间闭曲面, \(V\) 为其围成的立体,\(P,Q,R\) 且有一阶连续偏导数,则 \[\oint_SP(x,y,z)dydz+Q(x,y,z)dzdx+R(x,y,z)dxdy=\iiint_V\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial Q}{\partial z}\right)dxdydz\]
或者表示成向量形式的散度公式:
\[\oint_S\vec{F}\cdot\vec{n}dS=\iiint_V\text{div}\vec{F}dv\]
证明:我们只需要证明 \(\displaystyle \oint_SR(x,y,z)dxdy=\iiint_V\frac{\partial R}{\partial z}dv\) 即可,其余的证明类似。
我们假设 \(S\) 如图
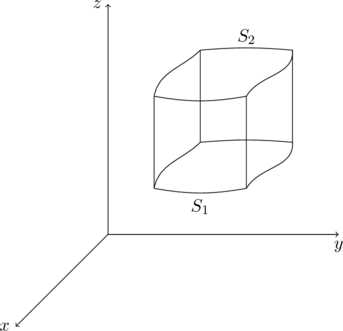
由下曲面 \(S_1\),上曲面 \(S_2\) 及平行于 \(z\) 轴的四个曲面 \(S_3,S_4, S_5,S_6\) 组成,
所以\[\oint_SR(x,y,z)dxdy=\left(\iint_{S_1}+\iint_{S_2}+\iint_{S_3}+\iint_{S_4}+\iint_{S_5}+\iint_{S_6}\right)R(x,y,z)dxdy\]
由曲面积分的定义
\[\iint_SR(x,y,z)dxdy=\iint_SR(x,y,z)\vec{k}\cdot\vec{n}dS=\iint_SR(x,y.z)\cos\gamma dS\]
因为曲面 \(S_3,S_4, S_5,S_6\) 与 \z\) 平行,所以它们的法向量与 \(\vec{k}\) 垂直,即 \(\vec{k}\cdot\vec{n}=0\),所以这几个曲面上的积分为 \(0\)。
假设 \(S_1: z=g_1(x,y), S_2: z=g_2(x,y)\),由曲面积分的定义与计算公式,我们有
\[\begin{align*}\oint_SR(x,y,z)dxdy&=\int_{S_1}R(x,y,z)dxdy+\int_{S_2}R(x,y,z)dxdy\\ &=\int_{S_1}R(x,y,z)\vec{k}\cdot\vec{n}dS+\int_{S_2}R(x,y,z)\vec{k}\cdot\vec{n}dS\\ &=-\iint_{D_{xy}}R(x,y,g_1(x,y))dxdy+\iint_{D_{x,y}}R(x,y,g_2(x,y))dxdy\end{align*}\]
这里 \(S_1\) 的符号是负的,是因为 \(S_1\) 的法向量指向下方,它与 \(\vec{k}\) 方向相反。由三重积分的计算公式
\[\begin{align*}\oint_SR(x,y,z)dxdy&-\iint_{D_{xy}}R(x,y,g_1(x,y))dxdy+\iint_{D_{x,y}}R(x,y,g_2(x,y))dxdy\\ &=\iint_{D_{xy}}(R(x,y,g_2(x,y))-R(x,y,g_1(x,y)))dxdy\\ &=\iint_{D_{xy}}\frac{\partial R}{\partial z}\Big|_{g_1(x,y)}^{g_2(x,y)}dxdy=\iint_{D_{x,y}}\int_{g_1(x,y)}^{g_2(x,y)}\frac{\partial R}{\partial z}dzdxdy\\ &=\iiint_V\frac{\partial R}{\partial z}dV\end{align*}\]
证毕!
由高斯公式,我们就可以利用三重积分来计算闭曲面上的曲面积分。实际上,即使不是闭曲面,我们也可以利用高斯公式来计算。
另外,我们需要注意的是,定理的条件是闭曲面外侧,如果是内侧,则积分符号为负。
的我们来看两个例子。
例1:求积分 \(\displaystyle\oint_S(x-y)dxdy+(y-z)xdydz\),其中 \(S\) 是柱面 \(x^2+y^2=1\) 及平面 \(z=0,z=3\) 所围成的闭曲面的外侧。
解:这里\(P(x,y,z)=(y-z)x, Q(x,y,z)=0, R(x,y,z)=x-y\),曲面外侧,所以可以直接应用高斯公式
\[\begin{align*}\oint_S(x-y)dxdy+(y-z)xdydz&=\iiint_V\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right)dV\\ &=\iiint_V\left(\frac{\partial }{\partial x}((y-z)x)+\frac{\partial }{\partial z}(x-y)\right)dV\\ &=\iiint_V(y-z)dV\end{align*}\]
因为这个闭曲面所围成的部分是圆柱体,所以应用柱坐标来计算三重积分比较简便,
\[\begin{align*}\iiint_V(y-z)dV&=\int_0^{2\pi}\int_0^1\int_0^3(r\sin \theta-z)rdzdrd\theta\\ &=\int_0^{2\pi}\int_0^1\left(r^2\sin\theta z-\frac{1}{2}rz^2\right)\Big|_0^3drd\theta\\ &=\int_0^{2\pi}\int_0^1\left(3r^2\sin\theta-\frac{9}{2}r\right)drd\theta\\ &=\int_0^{2\pi}\left(r^3\sin\theta-\frac{9}{4}r^2\right)\Big|_0^1d\theta\\ &=\int_0^{2\pi}\left(\sin\theta-\frac{9}{4}\right)d\theta=\left(-\cos\theta-\frac{9}{4}\theta\right)\Big|_0^{2\pi}\\ &=-\frac{9}{2}\pi\end{align*}\]
下一个例子,我们看一下如何利用高斯公式求一个开曲面的曲面积分。我们先添加一个辅助曲面将开曲面变成闭曲面,然后利用高斯公式计算闭曲面上的积分,最后再减去辅助曲面上的积分,就得到我们所求的曲面积分。
例2:求曲面积分 \(\displaystyle\iint_S\left(-\frac{1}{3}x^3+e^{z^2}\right)dydz+\left(-\frac{1}{3}y^3+x\tan z\right)dzdx+4zdxdy\),其中 \(S\) 为 \(z=x^2+y^2\) 在平面 \(z=4\) 以下的部分,上侧。
解:这是一个开曲面,我们给它加上一个盖子 \(S_1: z=4, x^2+y^2\le 4\) ,法向量朝下,组成一个闭曲面,
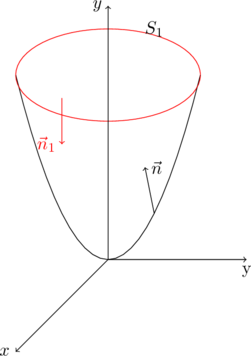
这个闭曲面的法向量是朝内的,所以
\[\begin{align*}\iint_S+\iint_{S_1}&=-\iiint_V\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial Q}{\partial z}\right)dxdydz\\ &=\iiint_V(-x^2-y^2+4)dV\end{align*}\]
这个积分区域的投影是圆 \(x^2+y^2\le 4\),下曲面是 \(z=x^2+y^2=r^2\),上曲面是 \(z=4\),所以利用柱坐标计算,\[V=\{(r,\theta,z)|0\le \theta\le 2\pi, 0\le r\le 2, r^2\le z\le 4\}\]
我们有
\[\begin{align*}\iiint_V(-x^2-y^2+4)dV&=\int_0^{2\pi}\int_0^2\int_{r^2}^4(4-r^2)rdzdrd\theta\\ &=\int_0^{2\pi}\int_0^2\int_{r^2}^4r(4-r^2)z\Big|_{r^2}^4drd\theta\\ &=\int_0^{2\pi}\int_0^2\int_{r^2}^4r(16-8r^2+r^4)drd\theta\\ &=\int_0^{2\pi}\int_0^2(8r^2-2r^4+\frac{1}{6}r^6)\Big|_0^2d\theta=\frac{32}{5}\theta\Big|_0^{2\pi}\\ &=\frac{64}{5}\pi\end{align*}\]
现在计算辅助曲面 \(S_1\) 的上积分,因为 \(S_1: z=4, x^2+y^2\le 4\),所以 \(dz=0\)。又因为它的法向量朝下,所以积分号为负,
\[\iint_{S_1}\left(-\frac{1}{3}x^3+e^{z^2}dydz+\left(-\frac{1}{3}y^3+x\tan z\right)dzdx+4zdxdy\right)=-\iint_{x^2+y^2\le 4}16dxdy=-16\cdot 4\pi\]
这里,\(1\) 的积分就是平面区域的面积,而圆 \(x^2+y^2\le 4\) 的面积为 \(4\pi\)。
所以
\[\begin{align*}\iint_S\left(-\frac{1}{3}x^3+e^{z^2}\right)dydz&+\left(-\frac{1}{3}y^3+x\tan z\right)dzdx+4zdxdy\\ &=-\iiint_V\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial Q}{\partial z}\right)dxdydz\\ &\quad-\iint_{S_1}Pdydz+Qdzdx+Rdxdy\\ &=-\frac{64}{5}\pi+64\pi=\frac{256}{5}\pi\end{align*}\]
