Stokes 公式是空间曲线积分的基本定理。它的结论是空间上闭曲线的积分可以用一个曲面积分来计算,这个曲面以这个闭曲线为边界。
1,曲面的正向边界(右手法则):我们的四个指头指向曲面边界前进的方向,那么拇指的指向就是曲面法向量的正向。
2,定理 (斯托克斯,Stokes公式):设 \(S\) 为有向曲面,\(L\) 为其正向边界,\(P,Q,R\) 在 \(S\) 及其边界上有一阶连续偏导数,则
\[\oint_LPdx+Qdy+Rdz=\iint_S\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)dydz+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)dzdx+\left(\frac{\partial Q}{\partial x}-\frac{\partial Q}{\partial z}\right)dxdy\]
写成向量形式 \[\oint_L\vec{F}\cdot d\vec{r}=\iint_S\text{curl}\vec{F}\cdot\vec{n}dS\]
证明:不失一般性,我们假设曲面的方程为 \(z=g(x,y)\),曲面的边界为 \(L\),\(L\) 在 \(xOy\) 平面上的投影为 \(L_1\),\(L_1\) 的内部为 \(D\),
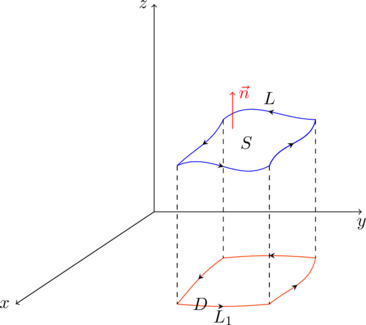
若 \(L_1\) 的参数方程为 \(L_1: \vec{r}(t)=(x(t), y(t)), a\le t\le b\),则 \(L\) 的参数方程为 \(L: \vec{r}(t)=(x(t), y(t), g(x(x),y(t)))\),那么由曲线积分的计算公式,
\[\begin{align*}\oint_LPdx+Qdy+Rdz&=\int_a^b\left(P,Q,R\right)\cdot\left(x'(t),y'(t),z'(t)\right)dt\\ &=\int_a^b\left[P\frac{dx}{dt}+Q\frac{dy}{dt}+R\left(\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{dt}\right)\right]dt\\ &=\int_a^b\left[\left(P+\frac{\partial z}{\partial x}\right)\frac{dx}{dt}+\left(Q+\frac{\partial z}{\partial y}\right)\frac{dy}{dt}\right]dt\\ &=\oint_{L_1} \left(P+\frac{\partial z}{\partial x}\right)dx+\left(Q+\frac{\partial z}{\partial y}\right)dy\\ &=\iint_D\left[\frac{\partial}{\partial x}\left(Q+\frac{\partial z}{\partial y}\right)-\frac{\partial }{\partial y}\left(P+\frac{\partial z}{\partial y}\right)\right]dA\end{align*}\]
注意,倒数第二个积分是在 \(L_1\) 上进行,而最后一个等式是应用了平面上的格林公式。
注意到 \(P,Q,R\) 都是 \(x,y,z\) 的函数,而 \(z\) 又是 \(x,y\) 的函数,所以
\[\frac{\partial}{\partial x}\left(Q+\frac{\partial z}{\partial y}\right)=\frac{\partial Q}{\partial x}+\frac{\partial Q}{\partial z}\frac{\partial z}{\partial x}+\frac{\partial R}{\partial x}\frac{\partial z}{\partial y}+\frac{\partial R}{\partial z}\frac{\partial z}{\partial x}\frac{\partial z}{\partial y }+R\frac{\partial^2 z}{\partial x\partial y}\]
\[\frac{\partial }{\partial y}\left(P+\frac{\partial z}{\partial y}\right)=\frac{\partial P}{\partial y}+\frac{\partial P}{\partial z}\frac{\partial z}{\partial y}+\frac{\partial R}{\partial y}\frac{\partial z}{\partial x}+\frac{\partial R}{\partial z}\frac{\partial z}{\partial y}\frac{\partial z}{\partial x }+R\frac{\partial^2 z}{\partial y\partial x}\]
相减后,最后两项相互抵消,剩下六项,
\[\begin{align*}&\iint_D\left[\frac{\partial}{\partial x}\left(Q+\frac{\partial z}{\partial y}\right)-\frac{\partial }{\partial y}\left(P+\frac{\partial z}{\partial y}\right)\right]dA\\ &\qquad =\iint_D\left(\frac{\partial Q}{\partial x}+\frac{\partial Q}{\partial z}\frac{\partial z}{\partial x}+\frac{\partial R}{\partial x}\frac{\partial z}{\partial y}-\frac{\partial P}{\partial y}-\frac{\partial P}{\partial z}\frac{\partial z}{\partial x}-\frac{\partial R}{\partial y}\frac{\partial z}{\partial x}\right)dA\\ &\qquad =\iint_D\left[\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)+\left(\frac{\partial Q}{\partial z}-\frac{\partial R}{\partial y}\right)\frac{\partial z}{\partial y}+\left(\frac{\partial R}{\partial x}-\frac{\partial P}{\partial z}\right)\frac{\partial z}{\partial x}\right]dA \\ &\qquad =\iint_D\left[\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)+\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)\left(-\frac{\partial z}{\partial y}\right)+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)\left(-\frac{\partial z}{\partial x}\right)\right]dA \\ &\qquad =\iint_S\left[\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\right]\cdot \left(-\frac{\partial z}{\partial x},-\frac{\partial z}{\partial y}, 1\right)dxdy\\ &\qquad =\iint_S\text{curl} \vec{F}\cdot\vec{n}dS\end{align*}\]
这是因为 \(\text{curl} \vec{F}=\left\{\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\right\}\),\(\vec{n}dS=\left(-\frac{\partial z}{\partial x},-\frac{\partial z}{\partial y}, 1\right)dxdy\),所以
\[\begin{align*}\oint_L\vec{F}\cdot d\vec{r}&=\iint_S\text{curl}\vec{F}\cdot\vec{n}dS\\ &=\iint_S\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)dydz+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)dzdx+\left(\frac{\partial Q}{\partial x}-\frac{\partial Q}{\partial z}\right)dxdy\end{align*}\]
这个定理给出了空间闭曲线上的曲线积分与曲面积分之间的关系。依据这个定理,我们可以将一个曲面积分换成另一个更简单的曲面积分,只要这两个曲面的具有相同的边界即可。
