我们之前在讲对坐标的曲线积分的定义的时候,曾经给出这么一个例子:
\[\int_L2xydx+x^2dy\] 沿三条曲线 \(L_1:y=x^2, L_2: y=\sqrt{x}\) 及 \(L_3:\) 从原点到 \((1,0)\) 再到 \((1,1)\) 的积分,从 \((0,0)\) 点到 \((1,1)\) 点的积分完全一样。
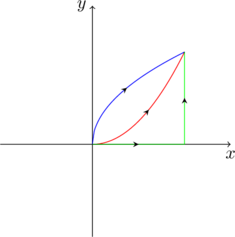
我们看到这三条曲线的起点与终点都是相同的,这就给出了一个问题:是不是这个积分只与起点与终点有关,而与路径无关?
1,曲线论基本定理给出了,\[\int_L\nabla f\cdot d\vec{r}=f(B)-f(A)\]也就是说,保守场的积分与路径无关,只与曲线的起点与终点有关。
我们给出这样的定义
2,积分与路径无关:若 \(\displaystyle\int_{L_1}\vec{F}\cdot\vec{r}=\int_{L_2}\vec{F}\cdot\vec{r}\) 对所有起点与终点相同的 \(L_1, L_2\) 成立,我们称曲线积分与路径无关。
3,曲线积分与路径无关的条件:下列条件是等价的
- \(\displaystyle\int_{L}\vec{F}\cdot\vec{r}\) 与路径无关;
- \(\vec{F}=\nabla f \);
- 平面上 \(\displaystyle\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\) ,或者立体上 \[\displaystyle\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x},\frac{\partial P}{\partial z}=\frac{\partial R}{\partial x},\frac{\partial Q}{\partial z}=\frac{\partial R}{\partial y}\]
- 沿任一闭曲线积分为 \(0\)。
证明:我们已经证明了第二条与第三条等价。由曲线积分基本定理,我们得到第二条能推出第一条。
现在我们证明第一条能推出第四条。

因为 \(\int_{L_1}\vec{F}\cdot d\vec{r} =\int_{L_2}\vec{F}\cdot d\vec{r}\),,而且\(L_1\)与 \(L_2\) 的反向组成一个闭曲线 ,我们记 \(L=L_1-L_2\),所以
\[\int_{L_1}\vec{F}\cdot d\vec{r} -\int_{L_2}\vec{F}\cdot d\vec{r}=0\quad\Rightarrow\quad \oint_L\vec{F}\cdot d\vec{r}=0\]
所以第一个条件能够推出第四个条件。现在证明第四个条件能推出第二个条件。
因为沿任一闭曲线的积分为 \(0\),由格林公式 \(\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\)。这就是第二个条件。如果是空间曲线,我们需要后面的 Stokes 定理。
我们可以利用与路径无关来求一些曲线积分。
例1:计算 \(\int_{(1,1)}^{(2,3)}(x+y)dx+(x-y)dy\)。
解:我们有
\[\frac{\partial P}{\partial y}=1, \frac{\partial Q}{\partial x}=1\]
所以 \(\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\),曲线积分与路径无关。我们选取路径
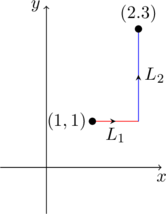
\(L_1: y=1, dy =0\),\(x\) 从 \(1\) 到 \(2\);\(L_2:x=2, dx=0\),\(y\) 从 \(1\) 到 \(3\)。所以积分为
\[\begin{align*}\int_{(1,1)}^{(2,3)}(x+y)dx+(x-y)dy&=\int_{L_1}(x+y)dx+(x-y)dy+\int_{L_2}(x+y)dx+(x-y)dy\\ &=\int_1^2(x+1)dx+\int_1^3(2-y)dy\\ &=\left(\frac{x^2}{2}+x\right)\Big|_1^2+\left(2y-\frac{y^2}{2}\right)\Big|_1^3\\ &=\frac{5}{2}\end{align*}\]
如果积分与路径无关,那么我们可以选取最容易计算的路径来计算曲线积分。通常选取 \(x\) 为常数和 \(y\) 为常数这样的路径,会大大简化计算过程。
