我们考虑某单位时间内流体通过曲面的流量问题。可以把问题想像为,一段时间内,河里的水流过一张渔网的流量。
1,流体通过曲面的流量:假设流体的速度向量为 \(\vec{F}(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z))\),曲面的法向量为 \(\vec{n}=\vec{n}(x,y,z)\)。这是因为,在不同的点,法向量的表达式不一样。
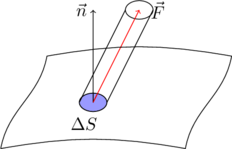
我们现在来推导流量的计算公式。
如同之前其它的积分推导一样,我们先将曲面划分成很小的一块块小曲面,在每个小曲面上,先计算流量的近似值,然后将曲面划分更细,近似程度越高,它的极限就是流量的精确值。
在 \(\Delta S_i\) 这个小曲面上,因为曲面的面积很小,速度向量近似于常向量,在此小曲面片上,任一取一点 \((x_i^*,y_i^*,z_i^*)\) 的速度向量 \(\vec{F}(x_i^*,y_i^*,z_i^*)\) 作为通过这整个小曲面片上的速度向量。从图形中我们可以看出,柱体的体积等于底面积乘以高,底面积为 \(\Delta S_i\),高等于 \(\vec{F}\) 在 \(\vec{n}\) 上的投影 \(\vec{F}\cdot \vec{n}\),所以,若 \(\vec{n}\) 为单位向量,通过 \(\Delta S_i\) 的流量\(\Delta \Phi_i\) 近似于
\[\Delta \Phi_i\approx \vec{F}(x_i^*,y_i^*,z_i^*)\cdot \vec{n}\Delta S_i\]
所以通过整个曲面的流量近似于
\[\Phi=\sum_{i=1}^n\Phi_i\approx \sum_{i=1}^n\vec{F}(x_i^*,y_i^*,z_i^*)\cdot \vec{n}\Delta S_i\]
将面面划分更细,使得每一个小曲面的面积趋于 \(0\),也就是取极限 \(\Delta S\to 0\),这里 \(\Delta S\) 是所有小曲面里面面积最大的那一块的面积。我们就得到了流量的精确值
\[\Phi=\lim_{\Delta S\to 0}\sum_{i=1}^n\vec{F}(x_i^*,y_i^*,z_i^*)\cdot \vec{n}\Delta S_i\]
我们再次看到了和式的极限,我们将它记作积分
\[\iint_S\vec{F}(x,y,z)\cdot\vec{n}dS=\lim_{\Delta S\to 0}\sum_{i=1}^n\vec{F}(x_i^*,y_i^*,z_i^*)\cdot \vec{n}\Delta S_i\]
2,向量场的曲面积分:我们将
\[\iint_S\vec{F}(x,y,z)\cdot\vec{n}dS=\lim_{\Delta S\to 0}\sum_{i=1}^n\vec{F}(x_i^*,y_i^*,z_i^*)\cdot \vec{n}\Delta S_i\]
称为对向量场的曲面积分,或者称为流量积分。对于流量问题,我们可以直接利用这个积分来计算。
3,对坐标的曲面积分:我们可以将向量场的曲面积分化为对坐标的曲面积分。假设 \(|\vec{n}|=1\),即它是单位法向量,那么它的方向余弦分别为 \(\cos \alpha, \cos\beta,\cos\gamma\),法向量可以直接写成 \(\vec{n}=(\cos \alpha, \cos\beta,\cos\gamma)\)。所以曲面积分为
\[\begin{align*}\iint_S\vec{F}(x,y,z)\cdot\vec{n}dS&=\iint_S(P(x,y,z),Q(x,y,z),R(x,y,z))\cdot(\cos \alpha, \cos\beta,\cos\gamma)dS\\ &=\iint_S(P(x,y,z)\cos \alpha+Q(x,y,z)\cos\beta+R(x,y,z)\cos\gamma)dS\end{align*}\]
若曲面的方程为 \(z=g(x,y)\),则曲面的上侧法向量为 \((-g_x,-g_y,1)\),下侧法向量为 \((g_x,g_y,-1)\),则单位法向量为 \(\vec{n}=(\frac{-g_x}{\sqrt{1+g_x^2+g_y^2}},\frac{-g_x}{\sqrt{1+g_x^2+g_y^2}},\frac{1}{\sqrt{1+g_x^2+g_y^2}})\),而面积元 \(dS=\sqrt{1+g_x^2+g_y^2}dxdy\),我们通常取法向量分量为正的部分(这里是 \(z\) 分量为正,就是上侧)为曲面的正向,也就是说,三个方向分别取上侧、右侧和前侧为曲面的正向,所以 \[\iint_SR(x,y,z)\cos\gamma dS=\iint_SR(x,y,z)\frac{1}{\sqrt{1+g_x^2+g_y^2}}\sqrt{1+g_x^2+g_y^2}dxdy=\iint_{S}R(x,y,z)dxdy\]
这里 \(D_{xy}\) 是曲面在 \(xOy\) 平面的投影。
同理, 我们可以得到
\[\iint_{S} P(x,y,z)\cos \alpha dS=\iint_{S}P(x,y,z)dydz,\quad \iint_{S}Q(x,y,z)\cos \beta dS=\iint_{S}Q(x,y,z)dydz\]
我们看到这些积分,积分变量都是坐标变量,我们称之为对坐标的曲面积分。
